Learning Resources
Lesson
By now, you should be very comfortable with the task of sketching the graphs of quadratic functions. What is important though, is that you are able to readily visualize where, in a given quadratic function, the y-values are greater than, equal to or less than zero. Before proceeding with Focus C, we will look at this concept further.
Consider the graph of a linear function.
- Where, on that graph, will the y-values be greater than zero? Equal to zero? Less than zero?
- Will your answers follow the same pattern no matter what linear equation you consider?
It is imperative that you give these questions some serious thought before viewing the answers. Failure to do so may hinder your understanding of the Focus. If you are unsure of the answers, write down a few linear equations, draw their graphs and then try to answer the questions. Record your answers.
After you have completed the task, you may view the solutions.
Now let's move on to the graphs of quadratic functions.
- Where, on the graph, will the y-values be greater than, equal to or less than zero?
- Is there a pattern you can follow?
- Upon what do your answers depend?
Answer these questions before moving on. Failure to do so may hinder your understanding of the Focus. Since detailed explanations were provided for the linear graphs, you should have little difficulty coming up with responses to these questions.
After recording your results, you may verify your solutions.
Now you are ready to begin Focus C on pages 67 & 68 of your text. In this Focus you will work through two methods of solving quadratic inequalities. Although called a Focus, this activity has been set up somewhat as an Investigation. Proceed with Method 1 of the Focus. Do not begin Method 2 until instructed to do so.
Hints are offered for some of the steps. Use them only if you are experiencing difficulty.
Before proceeding with method 2, read the note on interval notation located in the margin on page 68 of your text. Also, when drawing your number lines, be aware of the fact that an open circle is used to represent an endpoint that is not included in the solution set. A closed circle is used to represent an endpoint that is included in the solution set.
Method 2 is known as the Number Line Method. Quite often, however, it is referred as the "Sign Graph" Method, which is what it will be referred to in this web text. Follow the steps outlined in your text as you progress through Examples 2 and 3. Do not proceed any further until you have completed the Focus and Focus Questions.
After the Focus is completed in its entirety, you may view a detailed explanation of the Sign Graph Method.
Notebook Entry: Write an explanation of interval notation. It may help to include a few examples. Write the interval notation for the following:
- x
2
- -2 < x < 3
- x
4
- 1
Graphing technology can be used to obtain the solutions to these inequalities. An example is demonstrated.
Example 1
Solve the inequality x2 + 7x + 10 > 0.
Solution.
- Enter the quadratic x2 + 7x + 10 into the Y= menu.
- Press 2nd MATH to obtain the TEST menu.
- Choose 3: > in the TEST menu. Hit ENTER. The greater than symbol will appear on the Y= screen. Press 0 so that x2 + 7x + 10 > 0 appears on the screen.
- Choose appropriate WINDOW settings; perhaps -10 and 10 for x and y min and max respectively.
- Press GRAPH and the number line will appear on the screen.
- Your graph should look as follows:
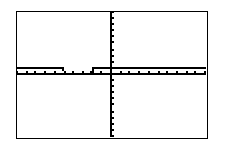
The solution of x2 + 7x + 10 > 0 is the intervals (-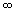
, -5) U (-3,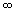). Note: the symbol U means the union of the two sets. Also note that -5 and -3 are not included in the solution since the inequality was to be solved for values strictly greater than zero, not greater than or equal to zero.
Activity
Focus questions page 69 #'s 1 - 3
C.Y.U. pages 69 & 70 #'s 4 - 10
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Express each of the following using interval notation.
(a) x < 5 (b) -2 < x < 6 - Solve each inequality below.
(a) -x2 + 2x -1 < 0 (b) 2x2 - x - 3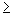 0
Solutions
1. (a) x ? (-, 5) (b) x ? (-2, 6)
2. (a) Roots: -(x2 - 2x + 1) = 0
-(x -1)(x -1) = 0
x = 1
Note that 1is a double root. Thus, there is no sign change as you pass
this root.
Choose a test value. Ex: when x = 0, the y-value is negative.
Solution: x ? (-,1) U (1, ). This can also be written as x 
1.
(b) Roots: (2x - 3)(x + 1) = 0
x = -1 or x = 
Test value: when x = 0, the y-value is negative.
Solution: x ? (-, -1] U [ , )