Learning Resources

Focus C: Solving Quadratic Inequalities

• A quadratic equation is of the form y = ax² + bx + c. The location of the
   y-values depends on whether a is positive or negative, as this determines whether the graph opens up or down. Naturally, the y-values will be equal to zero when x is the value of the x-intercept(s).
• If a is positive, the y-values are greater than zero for all values of x to the right of the largest x-intercept and to the left of the smallest one. The y-values are less than zero for all values of x that exist between the two x-intercepts. If, of course, the vertex is on the x-axis and the graph opens up, then y will never take on a negative value.
• If a is negative, the y-values are greater than zero for all values of x between the two x-intercepts. The y-values are less than zero for all values of x to the right of the largest x-intercept and to the left of the smallest one. If the vertex is on the x-axis and the graph opens down, y cannot have a positive value.

The graphs below illustrate these points.

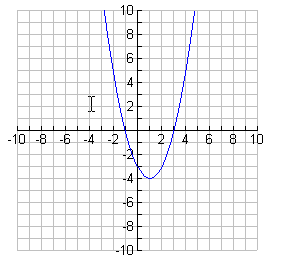
The y-value is equal to 0 when x is -1 and 3. The graph opens up.
The y-value is greater than 0 when for all values of x greater than 3 and less than -1.
The y-value is less than 0 for all values of x between -1 and 3.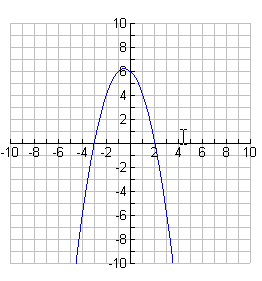

The y-value is equal to 0 when x is -3 and 2. The graph opens down.
The y-value is greater than 0 for all values of x between -3 and 2.
The y-value is less than 0 for all values of x less than -3 and greater than 2.