Learning Resources

Focus C: Solving Quadratic Inequalities

• The y-value will equal zero when x takes on the value of the x-intercept. This makes sense since every x-intercept has a y-coordinate of zero.
• Whether the y-values are greater than or less than zero depends upon the slope of the line, which is determined by the x-coefficient. 
• You should readily recall that lines having a positive slope rise upward to the right. Hence, If the slope is positive, the y-values will be greater than zero for all values of x that are greater than the value of the x-intercept. The y-values will be less than zero for all values of x that are less than the x-intercept. 
• Similarly, if the slope of the line is negative, the graph rises upward to the left. Thus, the y-values are greater than zero when the x-values are less than the value of the x-intercept. The y-values are less than zero for all values of x that are greater than the x-intercept.

The graphs below clearly illustrate this pattern.

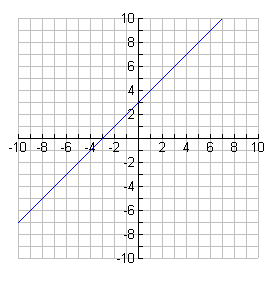
This graph has a positive slope, indicating that the x-coefficient in the equation is positive. The y-value is 0 when x = -3 (the x-intercept). The y-value is greater than 0 when x is greater than -3. The y-value is less than 0 when x is less than -3.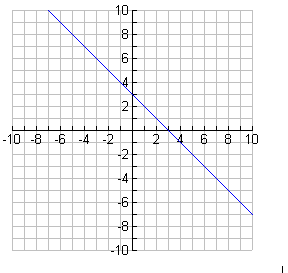

This graph has a negative slope, indicating that the x-coefficient in its equation is negative. The y-value is 0 when x is 3. The y-value is greater than 0 when x is less than 3. The y-value is less than 0 when x is greater than 3.