Learning Resources

Home »  » Courses » Mathematics » Advanced Mathematics 3207 (delisted) » Unit 02 » Set 02 ILO 01 » Explanation

Focus C: Solving Quadratic Inequalities

This is a much quicker process than Method 1, as you can tell the areas in which the y-values will be positive or negative without actually drawing the graph of the polynomial function.

First of all, you need to find the zeros of the function and locate these on a number line. The key component of this procedure hinges on the fact that a sign change can occur only at a root. This makes sense because, as you saw in Focus B, a graph crosses the x-axis at a root of the equation. Thus, it moves either from a positive region to a negative region or from a negative region to a positive region as it passes each root. In short, there is a sigh change as you move past each of the roots indicated on your sign graph.
 
Test one value on the sign graph. You may chose any value for x you wish except for one of the roots of the function. We already know that y is equal to 0 at these values of x. Zero is often the most convenient number to choose as a test value provided, of course, it is not one of the roots of the polynomial function. 

Once you have picked a value for x and determined whether y is positive or negative at that value, you can begin to create your sign graph. Remember to change the signs as you pass each x-intercept. It may be helpful to indicate the regions in which the y-values are greater than zero with the symbol +, and the regions in which they are negative with the symbol -.

There is, however, an exception here. Think about what happens at the x-axis when a double root exists. 

  • The graph just touches the x-axis at that point and does not cross. Thus, no sign change occurs. This holds true for any root that occurs an even number of times. 
  • It is important to remember this as you indicate the positive and negative regions on your sign graph. Always be aware of any double roots that exist.
  • As well, it is essential that you can use interval notation with ease. For example (2,10) represents all the values between, but not including 2 and 10. Whereas, [2,10) represents all the values from 2 to 10, including 2 but not 10. Similarly, (-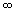, 5] represents all the values from negative infinity up to and including 5.