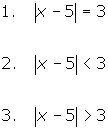Learning Resources
Lesson
This Focus is divided into two parts. Complete Part 1 by examining the number lines on page 171 and answering Focus Question #12. Do not proceed any further in your text until you are instructed to do so.
Recall that the absolute value of a number x is actually its distance from zero on the number line. This notion can help you solve linear equations and inequalities involving ![]() .
.
Essentially, there are three basic situations involving ![]() . Each one is illustrated below. The variable c is used to represent a constant value.
. Each one is illustrated below. The variable c is used to represent a constant value.
 = c
= c  < c
< c  > c
> c
Find all values of x that satisfy each equation or inequality below. Record your results.
 = 3. The distance from x to zero is exactly 3 units.
= 3. The distance from x to zero is exactly 3 units.  < 3. The distance form x to zero is less than 3 units.
< 3. The distance form x to zero is less than 3 units.  > 3. The distance from x to zero is greater than 3 units.
> 3. The distance from x to zero is greater than 3 units.
The correct solutions are available for you to verify your solutions.
From the previous examples, the following conclusions can be made.
- If
 = c, then x =
= c, then x = 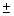 c.
c. - If
 < c, then -c < x < c. Essentially, x < c and x > -c.
< c, then -c < x < c. Essentially, x < c and x > -c. - If
 > c, then x > c or x < -c.
> c, then x > c or x < -c.
Notebook Entry:Record these rules, paying particular attention to the use of the words "and " and "or."
Equations and inequalities involving ![]() , where k is a constant, can be solved by interpreting
, where k is a constant, can be solved by interpreting ![]() as the distance from x to k on the number line.
as the distance from x to k on the number line.
As before, three situations exist. The three scenarios are given below.
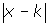 = c
= c 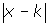 < c
< c 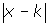 > c
> c
Using the rules previously established, find the values of x that satisfy each equation or inequality below.
Once the task is completed, you may verify your results.
Continue with part 2 of the Focus as outlined on pages 172 to 175 of the text. Pay close attention to each of the examples and the explanations offered. As well, note the use of number lines to aid each explanation.
Further details are provided for each of the four examples, should you require extra assistance. View this material only if you cannot follow a particular example after you have read it in its entirety. Otherwise the additional explanation will be meaningless.
Proceed with the Focus Questions.
An additional example is provided below.
Activity
Focus Questions page 175 #'s 13 - 17
C.Y.U. page 176 #'s 18 - 20
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- How can you interpret the sentence
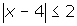 in terms of distance?
in terms of distance? - How can you interpret the sentence
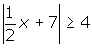 in terms of distance?
in terms of distance? - Solve for x:
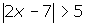 .
. - Solve for x:
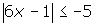 .
.
Solutions
- The distance from x to 4 is less than or equal to two units.
- The distance from
 x to -7 is greater than or equal to four units.
x to -7 is greater than or equal to four units. 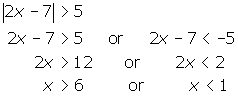
- By inspection, it is obvious that no solution exists.
- Regardless the expression of which you are evaluating the absolute value, you will never end up with a negative result. Thus, it is impossible to find a value of x such that the absolute value of 2x - 7 will be -5 or less.
- Some of you may not have recognized this fact, and actually solved the inequality. Upon examination of your answer, however, you will realize that it makes no sense.
- Your solution, if you solved the inequality, should have been x
 -
-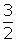 and
and
x 1. There is no value of x that satisfies these conditions.
1. There is no value of x that satisfies these conditions.