Learning Resources

Focus K: Absolute-Value and Inequalities

Example 3

• Previously, when working with rational expressions, you divided a sign graph into distinct intervals. It is important that you understand that this particular procedure is only used when one side of the inequality is zero. Since this is not the case in this example, this procedure is not applicable.
  
   
• Notice that when the absolute value sentence is rewritten as two inequalities, the absolute value notation is no longer used.
• Multiplication by the LCD gives two related inequalities. Because the sentence is based on "<," they can be expressed as two sentences using the word "and."
• As well, two cases must be considered; the LCD as a positive value and the LCD as a negative value. There is no need to consider the case when the LCD is zero, since if this were so, the expression would be undefined.
• Don't forget that the "sense" of an inequality changes when you multiply by a negative number.
• It is important that the two results be considered together. In Case 1, for example, the result is 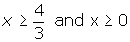. The solution that satisfies both inequalities is x 0.
• You can verify the result of this question on your graphing calculator. Plot the graphs of 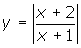and y = 2. Because the sentence uses 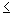, look for places where the graphs intersect and places where the rational equation is below the horizontal line.