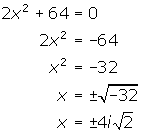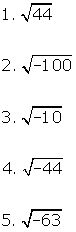Learning Resources

Home »  » Courses » Mathematics » Advanced Mathematics 3207 (delisted) » Unit 05 » Set 01 ILO 01 » Go to Work

Lesson

Investigation 1: Number Systems

During this investigation you will be working with the number systems you have explored in previous years. The number system you choose will depend upon the application you are to investigate. Although the Investigation is straight forward, it is an important one as it sets the stage for the need to explore the concept of imaginary numbers.

Carry out the procedure for Investigation 1 on page 272 of your text. When completing Step C, read the "Think about ..." in the margin. Hints and suggestions are provided for a couple of steps, should you experience difficulty.

Answer Investigation Questions #'s 1 to 7.

Note: There are three definitions given in the margin on page 273. Make the following additions and/or corrections as noted below.

Complex number: Add, to the given definition, the fact that a complex number is in the form a + bi, where a and b are real numbers, and i is the imaginary unit. 

The definition given for an imaginary number is actually the definition of a "pure imaginary number."

Notebook Entry: Describe the relationship between the number of x-intercepts that exist for a quadratic equation and the corresponding description of the roots. As well, making the adjustments noted above, record definitions for the following terms:

  • complex number
  • pure imaginary number
  • imaginary unit
Focus A: Working With Imaginary Numbers

This Focus offers a review of work with imaginary numbers. Before attempting the Focus, it is essential that you understand the imaginary unit introduced in Investigation Question #3. The imaginary unit, you will recall, is developed from a solution to an equation like x2 = -1.

To be successful with this Focus, it is also essential that you have a solid understanding of the process of simplifying radicals. Note that when writing imaginary numbers containing radicals, the imaginary unit is written first. For example, can be simplified as . This is the preferred way to express the answer, as opposed to . The latter expression can be confusing as it it difficult to tell if the imaginary unit, i, is under the radical sign or outside of it, as it should be.

Simplify the following radicals.

Check your solutions.

Some examples are provided below.

Your TI-83 Plus calculator can evaluate radicals, the solution to which are imaginary numbers. For example, suppose you are to evaluate . You saw from your previous work that the answer is 10i. To verify this using your calculator, follow the instructions below.

  • Press MODE.
  • Scroll down to Real and change it to the feature a + bi. This is the required setting for working with imaginary and complex numbers.
  • Go to the Home Screen and enter .
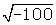  • Press ENTER.

You can also add, subtract, multiply, and divide imaginary numbers on your calculator. To enter imaginary numbers into the graphing calculator, follow the instructions below.

  • Press MODE.
  • Scroll down to Real and change it to the feature a + bi.
  • To enter an imaginary number such as 4i, enter 4, followed by i. The key for this is located above the decimal key. Of course, you have to press 2nd to select this key.

Although your calculator does many functions for you, it is imperative that you understand how to add, subtract, multiply, and divide imaginary numbers manually. As well, you must be proficient at simplifying radicals.

You already know that i 2 = -1. How can you use this fact to help you evaluate each of the following?

  1. i 3
  2. i 5
  3. i 9
  4. i 14
  5. i 40
  6. i 101

Do you see any patterns in your answers? Can you devise a rule?

Check your solutions.

Rules for simplifying imaginary numbers raised to various powers.

Adding and subtracting imaginary numbers is similar to adding like terms of polynomial expressions. Simply add the coefficients of the imaginary numbers. 3i + 8i, for example, is the equivalent of (3 + 8)i, which is 11i.

As well, multiplying imaginary numbers is similar to multiplying monomial expressions. To multiply imaginary numbers:

  • Multiply the coefficients.
  • Multiply the imaginary unit.
  • Simplify your answer using the fact that i 2 = -1.

Dividing imaginary numbers, however, is a little more complicated than the division of polynomial expressions. To divide imaginary numbers:

  • Divide the coefficients.
  • Subtract the exponents of i.
  • Remove all values of i from the denominator. To do so, you must rationalize, or "realize," the denominator.
  • Simplify.

If the denominator contains i raised to an even exponent, just simplify. The result will be either 1 or -1. If, however, the denominator contains i raised to an odd exponent, you will have to "realize" the denominator. To do so, multiply both the numerator and denominator by i. This will produce an even exponent of i in the denominator, which can be simplified to either 1 or -1, depending if the exponent is odd or even.

Using the above notes as a guideline, simplify the following. Record your results.

  1. 7i + 2i

  2. (3i )(5i )

Solutions.

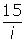
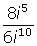
Read Focus A and answer the Focus Questions on pages 275 & 276 of your text.

Notebook Entry:Record the procedures for adding, subtracting, multiplying,  dividing, and working with powers of imaginary numbers. As well, record an example to accompany each situation.

Activity

Focus Questions page 275 #'s 8 - 14

C.Y.U. page 276 #'s 16 - 21

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

  1. Simplify .
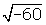  2. Evaluate i 20 + i 22.
  3. Evaluate (5i )(3i )(-2i ).
  4. Solve for x: 2x2 + 64 = 0.

Solutions

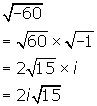
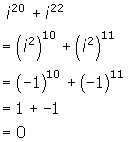
  3. (5i )(3i )(-2i ) = -30i 3 = (-30)(i 2)(i ) = (-30)(-1)(i ) = 30i