Learning Resources
Lesson
As an introduction to this Investigation, an explanation of radio signals and frequencies is provided.
The metric unit for cycles per second is Hertz, Hz. A washing machine, for example, operates at about a frequency of about 60 Hz, while other appliances operate at much higher frequencies. When an AM radio is tuned to, for example, 800 on the dial, it will amplify signals broadcast at a frequency of 800 kHz. This is read as "800 kilohertz"" since 1 kHz = 1000 Hz. Similarly, the number 95 on the FM dial represents 95MHz (megahertz) or 95 000 000 cycles per second.
Take a few moments to read the introduction to the section on page 258 of your text.
It is important for you to understand that musical notes can be represented graphically and that the equations of the functions represented can be determined.
Complete the Think about... box in the margin.
To be successful with Investigation 9 you will need to recall how to determine the period of a trigonometric function. A review of this concept, should you require one, is provided.
Proceed with the Investigation, completing each step as required. Hints and suggestions are provided in case you experience difficulty.
The Investigation Questions require you to make connections between period of the sum function and the periods of the functions being added. If you are having difficulty making connections, it might be helpful to convert the period measures to degrees. Convert them back to radians once the connection has been made.
Complete the Investigation Questions.
A summary of the Investigation is provided.
Activity
C.Y.U. pages 260 & 261 #'s 7 - 10
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
For each of the following, give the period of the combined function f(x) + g(x).
- f(x) = sin(2x) and g(x) = sin(3x).
- f(x) = sin(3x) and g(x) = sin(4x).
- f(x) = sin(3x) and sin(18x).
- f(x) = cos(
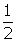x) and g(x) = cos(2x).
Solutions
Recall: The period of the combined function is the lowest common multiple of the of the periods of each individual function.
- The period of f(x) is
or 180° and the period of g(x) is 
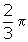or 120°. The LCM is 360° or 2. - The period of f(x) is 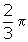or 120° and the period of g(x) is
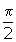or 90°. The LCM is 360° or 2. - The period of f(x) is 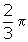or 120° and the period of g(x) is
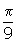or 20°. The LCM is 120° or 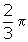. - The period of f(x) is 4 and the period of g(x) is . The LCM is 4.