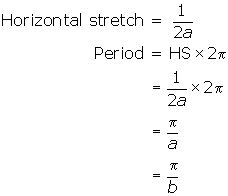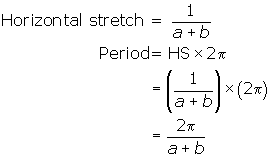Learning Resources

Investigation 9: Combining Functions

• The period of y = sin(ax) + sin(bx) is the lowest common multiple of the periods of y = sin(ax) and y = sin(bx). This pattern is true regardless of the number of trigonometric functions being combined.
• When a = b, the period of y = sin(ax) + sin(bx) is the same as the periods of y = sin(ax) and y = sin(bx).

Since a = b,    y = sin(ax) + sin(bx)
                        y = sin(ax) + sin(ax)
                        y = 2sin(ax)

Thus, when a = b, the amplitude is 2. It is doubled.

• sin(ax + bx) 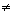sin(ax) + sin(bx).
• For y = sin(ax + bx), it is established that:

If a = b,    y = sin(ax + bx)
                y  = sin(ax + ax)
                y  = sin(2ax)

If a < b or a > b,    y = sin(ax + bx)
                              y = sin((a + b)x)