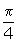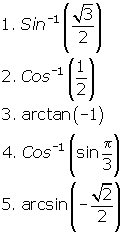Learning Resources
Lesson
The purpose of this Investigation, as its name suggests is to develop the inverse trigonometric functions. The Investigation is based on Linda's fear of heights and her desire to ride a Ferris wheel.
Graph paper is needed for this Investigation. Read the introduction and complete each step of the Investigation as outlined on pages 252 & 253 of your text. Hints and suggestions are provided for many of the steps, should you experience difficulty.
Before answering the Investigation Questions, answer the questions below to ensure your understanding of the Investigation.
- Evaluate sin-1
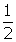. - Evaluate Sin-1.
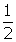You may verify your solutions.
Proceed with the Investigation Questions on page 253.
A summary of the Investigation is provided.
Notebook Entry: Record a definition of the principal inverse trigonometric functions y = Sin-1x, y = Cos-1x, and y = Tan-1x and state their respective domains and ranges. As well, explain the difference between the following:
- y = sin-1x and y = Sin-1x
- y = cos-1x and y = Cos-1x
- y = tan-1x and y = Tan-1x
Some additional examples are provided below.
Before attempting the Check your Understanding section, you will need the range for the reciprocal principal trigonometric inverse functions. Make a note of the table below in your exercise.
| Function | Range |
| y = Sec-1x |  |
| y = Csc-1x |  |
| y = Cot -1x |  |
Note: The range for y = Sec-1x and y = Csc-1x have not been universally agreed upon. The ranges given above are one possibility.
Carefully examine the solution to the problem below.
Evaluate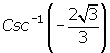 
.
A common mistake is to assume that, since sine is the reciprocal of cosecant, it is acceptable to rewrite the given expression as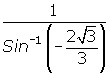 
.
The correct way to rewrite the given expression is shown below.
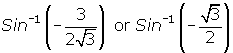
The following approach is probably the easiest to use when solving problems of this nature.
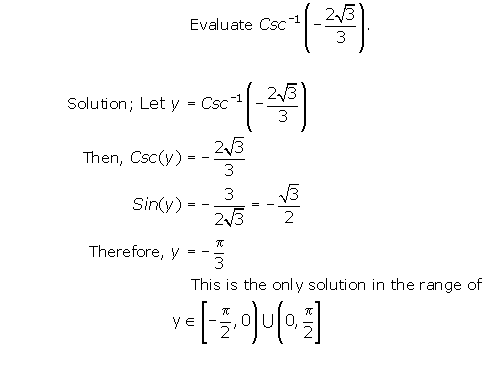
Activity
C.Y.U. pages 253 & 254 #'s 18 - 23
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
Give the exact value of each expression below.
Solutions
Note: All of these questions suggest use of the principal value. Thus, there is only one solution for each.
- You are looking for an angle for which the sine is
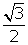. The solution must be in the range 
.
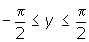Solution: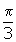
- You are looking for an angle for which the cosine is 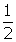. The solution must be in the range
.
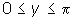Solution: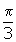 - You are looking for an angle for which the tangent is -1. The solution must be in the range
.
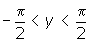Solution: -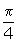
- Evaluate inside the brackets first to get Cos-1( 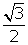). You are looking for an angle for which the cosine is 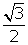. The solution must be in the range .
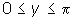Solution: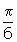
- You are looking for an angle for which the sine is -
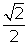. The solution must be in the range .
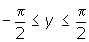Solution: -