Learning Resources

Investigation 8: Inverse Trigonometric Functions

1. You are looking for angles for which the sine  is 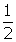. It is the equivalent of solving sinx = .
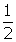   Solution: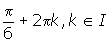
2. This is the equivalent of solving Sinx = 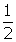. In this case, however, you are dealing with the principal inverse trigonometric function. Thus, you are looking for angles between - 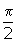and 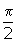, inclusive, for which the sine is 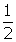. Remember the principal value is suggested by use of capital letters. Therefore, there is only one solution.
   Solution: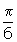 . This is the only answer that fits in the restriction.