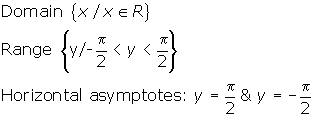Learning Resources

Investigation 8: Inverse Trigonometric Functions

Principal Inverse Trigonometric Functions:

• y = sinx does not have an inverse function. However, if you restrict the domain of y = sinx to values of x between - 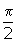and 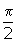inclusive, the restricted function, denoted y = Sinx has an inverse function. Its inverse is denoted y = Sin^-1x or y = arcsinx.
  
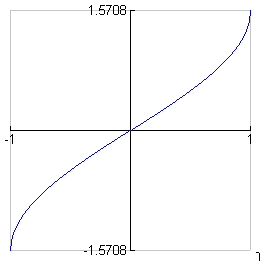
  y = Sin^-1x = arcsinx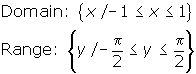
  
  
  
  
• y = cosx does not have an inverse function. However, if you restrict the domain of y = cosx to values of x between 0 and inclusive, the restricted function, denoted y = Cosx has an inverse function. Its inverse is denoted y = Cos^-1x or y = arccosx.
  
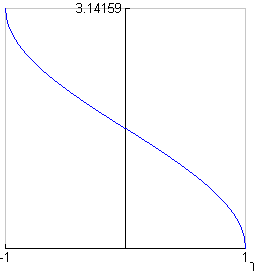
  y = Cos^-1x = arccosx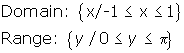
  
  
  
  
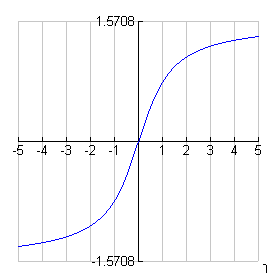
• y = tanx does not have an inverse function. However, if you restrict the domain of y = tanx to values of x between - 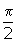and 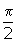, the restricted function, denoted y = Tanx has an inverse function. Its inverse is denoted y = Tan^-1x or y = arctanx. 
  
  y = Tan^-1x = arctanx