Learning Resources
Lesson
Transformations of y = sinx and y = cosx were thoroughly covered in Mathematical Modeling, Book 2. A brief review of the transformational form of a trigonometric function is provided for those who wish to use it. If you feel you do not require a review, you may proceed with the Focus.
Notebook Entry:Record a summary of the transformational form of a trigonometric function.
Before attempting the Focus, think about the key points required to sketch a periodic function. You should recall from Mathematics 2205 the following points.
- The amplitude represents the vertical stretch.
- The sinusoidal axis is the result of a vertical translation
- The horizontal translation represents a phase shift of the sine or cosine function. For cosine, you find a maximum point on the graph to determine the horizontal translation. For sine, it is determined by finding a point onto which (0, 0) is mapped.
- The period indicates the horizontal stretch.
The following example may serve to prepare you for the Focus.
Example 1
Mrs. Cashin is standing in a dory in Port aux Basque harbour. The boat is 1.2 meters from the sea floor in the trough of the wave. Two seconds later, the boat is on the crest of the wave two meters from the sea floor. Write the equation of the sea wave function, using sine and cosine, described below.
You are now ready to proceed with Focus A, Part I. The questions are designed to help you review skills with graphing trigonometric functions in transformational form. Carefully read the description given in your textbook and determine the key components of the equation. You should sketch the required graphs by hand, then check them with a graphing calculator.
Remember, there are many possible answers to question (b) in Example 1. There is, however, an error in the answer presented for the sine function. At time t = 6, the function is decreasing, not increasing as stated in the text. Thus the equation that should have been attained is 
.
Answer the Focus Questions on pages 228 & 229 of the text.
Part 2
This part of the Focus involves the exploration of transformations to the tangent function encountered in Investigations 3 and 4. If you completed Part I of the Focus with little difficulty, you should have no trouble answering these Focus Questions. Basically, you are to extend to the tangent function the skills you have developed for graphing the sine and cosine functions.
An example of graphing the tangent function is provided below.
Activity
Focus Questions pages 228 & 229 #'s 1 - 3
Focus Questions page 230 #'s 4 - 6
C.Y.U. pages 230 - 232 #'s 7 - 12
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- What is the period of the tangent function?
- What is the maximum value of the tangent function?
- Given: f(x) = tanx g(x) = x -
h(x) =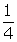 
x . Find f(h(g(x))) - Describe with words and a mapping rule, the transformations of y = tanx that will give
.
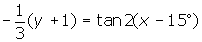Solutions
1. 
2. There is no maximum value.
3. 
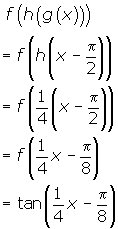
4.The function has undergone the following transformations.
- a reflection of y = tanx in the x-axis
- a vertical stretch of factor 3
- vertically translated 1 unit down
- horizontally translated 15° right
- it has a period of 90°
Mapping Rule: 