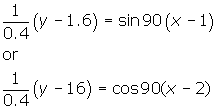Learning Resources

Focus A: Graphing Periodic Functions Using Transformations, Part I and Part II

Solution

• The amplitude of the function is found using 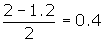. Thus the vertical stretch is 0.4.
• The sinusoidal axis is found using y = 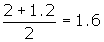. Thus, there is a vertical translation of 1.6.
• The horizontal stretch is determined by comparing the period of the given problem to that of y = sinx or y = cosx, which is 360°. The period evident in the given problem is 4 seconds. 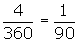which represents the horizontal stretch.
• The horizontal translation is determined differently for the sine and cosine functions. For sine, (0, 0) is mapped to the point (1, 1.6). Thus, the horizontal translation is 1. For cosine, the first maximum occurs when x is 2. Thus, the horizontal translation is 2. 
• There are many possible solutions for both the sine and cosine equations due to the fact that the horizontal translation for each can vary. A sample answer for each function is provided.