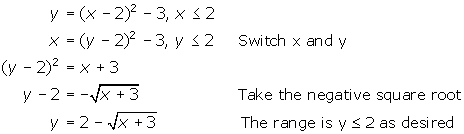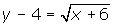Learning Resources

Home »  » Courses » Mathematics » Advanced Mathematics 3207 (delisted) » Unit 03 » Set 04 ILO 01 » Go to Work

Lesson

The section opener explores the relationship between initial speed and the length of a skid mark. Read the introduction to the activity outlined on page 157 of your text. Do not answer any of the related questions just yet. 

  • Without using your graphing calculator, can you make a conjecture about the type of graph that would be produced by the five ordered pairs?
  •  Can you at least predict the types of function that definitely would not be produced by these order pairs?
  • Is it possible for the graph to be linear? Quadratic? 

You will need to think back to your work in Mathematical Modeling, Book 3, to answer these questions.

Many of you may be convinced the graph is linear because the first level  differences are equal.  Explain why this is not the case. After writing your response, you may view the correct reason. 

  • Using the STAT feature, enter the data in two lists, L1 and L2, on your graphing calculator.
  • Adjust the WINDOW accordingly.
  • Create a graph of the data using the STAT PLOT feature.
  • Make a conjecture about the type of function represented.
  • How does your answer compare to your initial response? 

You will have an opportunity later, in Investigation 4, to make any necessary adjustments to your present conjecture. You may view sample screens if you need assistance with this task. 

Keep this graph in your calculator. You will need to refer to it again in Investigation Question #8.

Now that you have had some time to examine the data, you may proceed with the questions on page 157.

Investigation 4: The Square-Root Function

Proceed with the Investigation, carefully drawing the required graphs. You may check for hints and suggestions for each step if you are experiencing difficulty.

After Step B is completed, answer the following questions before moving on to the Investigation Questions.

  1. The graph of 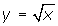is obviously not a reflection in the line y = x of the entire parabola y = x2. Which part of the parabola reflected in the line y = x results in the graph of ?
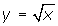  2. Why do you think you were instructed to use only the principal square root? What would the graph look like if you had graphed 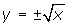? Would it have passed the Vertical Line Test? Would the graph represent a function?
  3. Will the square-root of a linear function always be the inverse of a quadratic function? Explain.

You may check your responses once you have completed the questions.

You may now proceed with the Investigation Questions. Question #8 refers you back to the graph you constructed in the section opener. If you have deleted this graph from your calculator, re-enter it as you will need to use it for comparison purposes. You are to determine an equation for this graph. There are many ways you can opt to approach this task. A few suggestions are provided if you are experiencing difficulty.

Focus H: Irrational Functions and Inverses

From Investigation 4, you saw that the graphs of functions and their inverses are reflections in the line y = x. A point (x, y), reflected in the line y = x, becomes the point (y, x). In other words, the x and y-values become interchanged. Since the x-values represent the domain of a function and the y-values represent the range, interchanging the x and y-values is, in essence, switching the domain and range.

It important to use the proper notation for inverse functions. The inverse of the function f(x) is denoted f -1(x). Thus from the information in the above paragraph, you can conclude that the domain of f(x) becomes the range of
f -1(x). The range of f(x) becomes the domain of f -1(x).

Before moving on, answer the following questions in your notebook to ensure your understanding thus far.

  1. If a function f(x) has domain {x / x > 5} and range {y / y > 0}, what is the domain of f -1(x)?
  2. Given f(x) = 2x - 4. What is the range of f -1(x)?
  3. Given 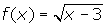. State the domain and range of f -1(x).

Once you have completed all questions, you may check your responses.

The relationship between a function, f(x) and its inverse function,  f -1(x), is that the domain of one is the range of the other, and vice-versa. In other words, the x-values of one become the y-values of the other. Knowledge of this fact can help greatly when trying to find the equation of  f -1(x), based on the equation of
f(x).

As a general rule, you can obtain the inverse of a function by exchanging x and y and then solving the equation for y. Use this information to help you find the inverse of each function below.

  1. f(x) = 2x - 5

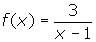
You may check your solutions once you have completed the task.

Consider the function f(x) = x2 - 4. You should recognize this is a parabola with vertex (0, -4) that opens upward.  From Investigation 4, you should realize that
f -1(x) will not be an inverse function, since reflecting this graph in the line y = x will produce a sideways parabola which fails the Vertical Line Test. For the inverse to be a function, it must be exactly half a parabola. This ensures the graph will pass the Vertical Line Test.

How do you obtain half a parabola? On what basis would you determine the restriction to be placed on the domain of the given parabolic function?

Look again at the function given above and answer the following questions.

  1. What point splits the parabola into exactly two pieces?
  2. Will both halves of the parabola have inverse functions?
  3. Write a suitable restriction for the domain of the function so that the inverse will also be a function. Is there more than one possible answer? Explain.

Correct responses are available to allow you to verify your thinking.

Restrict the domain of each function below so that its inverse will also be a function.

  1. y = 2x2 - 3

  2. y = (x+3)2

  3. y = (x - 1)2 + 4

You may view the correct responses once you have completed the task.

By now you should understand that if you were asked to find the inverse of the function f(x) = x2 - 3, the inverse would not be a function. That doesn't mean, however, that the equation of the inverse is impossible to determine. What it means is that, once found, this inverse equation would not be a function.

Let's find the inverse of the above function.

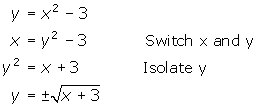
Notice that you are taking both the principal and negative square root of the expression, each resulting in a different equation. Each one represents half a parabola; the two combine to produce one complete parabola opening sideways. Obviously this is not a function as it fails the Vertical Line Test. 

Refer back to the original function again. To ensure the inverse is indeed a function, you must restrict the domain accordingly. There are two possible restrictions. We will look at each case individually.

Case 1: Restriction {x / x 0}. Given f(x) = x2 - 3, x 0, find f -1(x).

You must keep in mind the given restriction when finding the equation of the inverse. Here the domain of f(x) is x 0, Thus the range of f -1(x) must be
 {y / y 0}. This is what determines whether you will take the principal or negative square root. To obtain y-values that are greater than or equal to zero, the principal square root must be taken. The solution is shown below.

Case 2: Restriction {x / x 0}. Given f(x) = x2 - 3, x 0, find f -1(x).

In this case, the range of f -1(x) must be {y / y 0}.Thus, the negative square root must be taken. The solution is shown below.

You are now ready to proceed with the Focus. Read pages 158 to 160, paying close attention to the examples, and answer the Focus Questions. Refer back to the Web pages on this lesson if you are experiencing difficulty.

Notebook Entry: Record the process of finding the equation of the inverse. As well, record how to restrict the domain of a quadratic function to ensure its inverse is also a function.

An example similar to the Check Your Understanding question on pages 160-161 is done below.

A summary of Investigation 4 and Focus H is provided if you require clarification of points.

Activity

Focus Questions page 160 #'s 9 & 10

C.Y.U. pages160 & 161 #'s 11 - 17

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

  1. If the point (2, 8) is on the graph of f(x), what point must be on the graph of f-1(x)? Explain.
  2. Restrict the domain of f(x) = 3(x - 4)2 + 5 so that f-1(x) is also a function.
  3. Find the inverse of the function f(x) = (x - 2)2 - 3, x 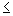2.
  4. Write the resulting function when 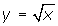is transformed 6 units left and 4 units up.

Solutions

  1. The point (8, 2) must be on the graph since f(x) and f-1(x) are reflections in the line y = x.
  2. Two answers are possible; x 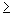4 or x 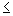4.