Learning Resources

Investigation 4: The Square-Root Function & Focus H: Irrational Functions and Inverses

By now you should understand that if you were asked to find the inverse of the function f(x) = x² - 3, the inverse would not be a function. That doesn't mean, however, that the equation of the inverse is impossible to determine. What it means is that, once found, this inverse equation would not be a function.

Let's find the inverse of the above function.

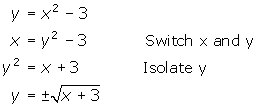
Notice that you are taking both the principal and negative square root of the expression, each resulting in a different equation. Each one represents half a parabola; the two combine to produce one complete parabola opening sideways. Obviously this is not a function as it fails the Vertical Line Test. 

Refer back to the original function again. To ensure the inverse is indeed a function, you must restrict the domain accordingly. There are two possible restrictions. We will look at each case individually.

Case 1: Restriction {x / x 0}. Given f(x) = x² - 3, x 0, find f ^-1(x).

You must keep in mind the given restriction when finding the equation of the inverse. Here the domain of f(x) is x 0, Thus the range of f ^-1(x) must be
 {y / y 0}. This is what determines whether you will take the principal or negative square root. To obtain y-values that are greater than or equal to zero, the principal square root must be taken. The solution is shown below.

Case 2: Restriction {x / x 0}. Given f(x) = x² - 3, x 0, find f ^-1(x).

In this case, the range of f ^-1(x) must be {y / y 0}.Thus, the negative square root must be taken. The solution is shown below.