Learning Resources

Investigation 4: The Square-Root Function & Focus H: Irrational Functions and Inverses

• Two functions are inverses of each other if they are reflections in the line
   y = x. This means each point (x, y) on the graph of f(x) is mapped onto the point (y, x).
• The domain of f(x) is the range of f ^-1(x) and the range of f(x) is the domain of f ^-1(x).
• To find the equation of the inverse, switch x and y, and solve for y.
• The inverse of a parabolic function is the square root of a linear function. This inverse will be a function only if the domain of the parabola is restricted properly.
• To restrict the domain of a parabola, you must identify its vertex. There are two possibilities for the restriction; x 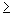the x-coordinate of the vertex or x 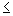the x-coordinate of the vertex.
• The graph of f(x) is a function if it passes the Vertical Line Test.
• You can tell, by examining the graph of f(x), whether or not f ^-1(x) will be a function. If the graph of f(x) passes the Horizontal Line Test, f ^-1(x) will be a function.
• The Horizontal Line Test states that if, when you draw a horizontal line through the graph of f(x), it touches in exactly one place, then the inverse will be a function. Obviously all parabolas opening up or down fail this test. This is why their inverses will not be functions unless you restrict their domains appropriately. Half a parabola will pass the Horizontal Line Test. Thus its inverse will be a function.