Learning Resources
Lesson
Investigation 1: The Pressure and Volume Relationship for a Gas
Before beginning the Investigation, complete the following activity so as to get a feel for the behaviour of rational functions in which the numerator is a constant.
Graph 
using technology.
If you are using your graphing calculator, change the mode from connected to dot to avoid connecting the graph in places where it is not appropriate. Using the TRACE and ZOOM features, record the behaviour of the function (i.e., the value y tends toward) when x becomes:
- increasingly further away from the origin, in either direction
- a number close to zero, tracing toward zero from the left
- a number close to zero, tracing toward zero from the right
The correct responses are provided for you to view after the task is completed.
Investigation 1 centres around the well known pressure-volume relationship for an ideal gas known as Boyle's Law, which states that the pressure and volume are inversely proportional. This means that as the value of one variable increases, the other decreases.
Hints and suggestions are provided for the various steps of the Investigation. Use these as directed by your on-line teacher.
Note:
- In reality, air only approximates an ideal gas.
- The data you collect will be modeled very well but not exactly by a function
.
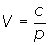As you answer the Investigation Questions, pay particular attention to the asymptotic behaviour of the function as the dependent variable tends to either zero or infinity.
Focus A: Functions of the Form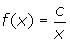 
This Focus presents the graph of the function and examines its asymptotic behaviour.
A good understanding of Investigation 1 will allow you to progress through the related questions with relative ease.
Take a few moments to read Focus A on page 129 of your text. Then complete the accompanying Focus questions.
Some guidance is provided for each of the Focus Questions should you experience difficulty.
When trying to identify an equation of a function as a transformation of , it is usually difficult to see the stretches.
However, it is helpful to remember that the basic function is satisfied by the points (-1, -1) and (1, 1).
As such, the two halves of the function at these points are separated diagonally by two grid-unit squares. If you notice this to be the case for a graph, then it is likely not stretched.
Be sure to pay particular attention to the "Think about ..." located in the margin on page 130. You will need an understanding of the concept presented as it resurfaces in Investigation 2.
An example, similar to the Check Your Understanding questions, is provided below.
Activity
Focus Questions page 129 #'s 3 & 4
C.Y.U. pages 129 - 132 #'s 5 - 12
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Examine the graph below. Write the equation of the function as a transformation of 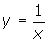, and state the following:
(a) the domain and range
(b) the equations of any existing asymptotes
(c) any existing intercepts
(d) where the graph is increasing and decreasing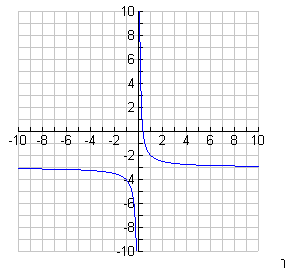
- Write a new equation after the function 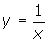has been transformed 2 units to the left and 3 units up.
- Write the equations of the horizontal and vertical asymptotes for the function
.
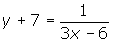Solutions
1.
- Equation:
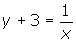
- Domain:
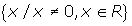; Range: 
- Horizontal asymptote: y = -3 ; Vertical asymptote: x = 0
- x-intercept (
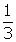, 0) - Increasing nowhere; Decreasing everywhere in the domain
2. 
3. Horizontal asymptote: y = -7; Vertical asymptote: x = 2