Learning Resources

Home »  » Courses » Mathematics » Advanced Mathematics 3207 (delisted) » Unit 02 » Set 05 ILO 04 » Go to Work

Lesson

Previously you have studied increasing and decreasing functions. As well, you saw that the vertex of a function indicates its maximum and/or minimum values. If you require a quick summary of these concepts, one is provided. There are many different ways to investigate the shape of a function. This section looks at the role that the slope of a function at a point plays in this analysis.

A function is graphed below.Record your answers to the following questions.

• Determine over which intervals the function is increasing? Decreasing?
• For what values of x is the function neither increasing nor decreasing?

Answers

With your on-line teacher's permission, you may choose to carry out this Investigation in pairs or small groups. Doing so, will provide opportunity for discussion of the conclusions you reach.

Follow the steps of the Investigation as outlined on pages 100 & 101 of your text and complete the accompanying Investigation Questions. If you are experiencing difficulty with the procedure, you may use the given hints before contacting your on-line teacher.  

Do not use a graphing calculator to draw the requested graphs. It is important that you have the results on graph paper for analysis.

• Step A   
• Step B
• Steps C & D
• Step E            

To help clarify your thinking, repeat the steps of the Investigation for the function f(x) = 6 + x - x². Check your results.

Activity

C.Y.U. pages 101 & 104 #'s 26 - 40

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

1. What can you conclude about the degree of the slope function compared to the degree of the original polynomial function?
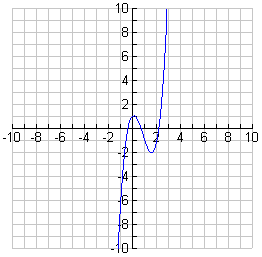
2. A polynomial function is graphed below. What conclusions can be made, about the graph of the slope function?

Solutions

1. The degree of the slope function is always one less than the degree of the original polynomial function.

2. The conclusions, along with their explanations, are given below.

• The original function is a positive cubic polynomial. Thus, the slope function is a positive quadratic.
• The graph of the original function is increasing over the intervals
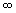  (-, -2.5) U (0.5, 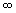) and decreasing over the interval (-2.5, 0.5). Thus, the graph of the slope function has positive y-values for all values of x from - 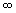to -2.5 and from 0.5 to 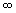. It has negative y-values for all values of x from -2.5 to 0.5.
• The maximum and minimum values of the original function occur when x is -2.5 and 0.5. Hence, these values will be the x-intercepts of the slope function.