
Learning Resources
Lesson
The purpose of this investigation is for you to discover the relationships between:
- the slopes of parallel lines
- the slopes of perpendicular lines
To do the investigation on the slopes of parallel and perpendicular lines you can follow the steps for Investigation 3 or you can use the Geometer's Sketch Pad interactive window provided. Regardless of the method you use, you will need the following materials to work on this lesson and the assigned activities:
- graph paper
- a ruler
Text method
The instructions are straightforward for this investigation. If you prefer, you can get in groups of two or three to complete this investigation.
In Step A, after you have the points plotted check that MATH is a square by measuring its sides and angles.
To calculate the slopes in Step B, you can either use the graph and count the blocks to find the rise over the run between the points or more effectively use the formula for slope. The formula for calculating the slope is given in the sidebar of your text. The subscripts are used to distinguish between the two points. Thus x1refers to the x-coordinate of the first point, and x2to the x-coordinate of the second point. For example to find the slope of the segment joining (-3 , 5) and (2, -4),use the formula as follows:
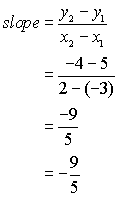
GSP Interactive method
The first interactive window investigates the relationship between the slopes of parallel lines. For instructions go here.
The second interactive window investigates the relationship between the slopes of perpendicular lines. For instructions go here.
Summary
The conclusions for this investigation are contained in Step C. If you have done it properly you should have arrived at the following:
- The slopes of parallel lines are equal.
- The product of the slopes of perpendicular lines is -1. Alternately you could say that the slopes of perpendicular lines are negative reciprocals of each other ( for example: ½ and -2, -¼ and 4, are negative reciprocals of each other).
Although not clearly stated in the investigation, the converses of the above statements are also true, viz.
- If the slopes of two lines are equal, then they are parallel.
- If the product of the slopes of two lines is -1 (i.e. they are negative reciprocals of each other), then they are perpendicular.
To complete the assigned activities you will also have to use the formula, which you learned in a previous course, for calculating the slopes of lines. It states that given the points A(x1 , y1) and B(x2 , y2) , the slope formula is:
![]()
Keep in mind that when conclusions such as these are based on the results of an experiment or an investigation and we think that these results will always occur based on the fact that many examples were used, we are using inductive reasoning. This does not conclusively prove the fact since if one counterexample can be found then the statement is not true. However, for now we will accept these statements as true.
Activity
Investigation Questions p.222 - 223. Complete 1, 2 and 3
Check Your Understanding p.223. Complete 4 to 9 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
- Prove that CDFE is a trapezoid (has only one pair of opposite sides parallel), given C(-8 , 4), D(4 , 10), F(5 , 3), E(-5 , -2). Are any of its angles right angles?
Click here for suggested solution.