Learning Resources
Lesson
The instantaneous rate of change is the slope of the tangent to a graph of continuous ordered pairs of data, at a particular point. For example, with a distance-time graph the slope of the tangent represents the speed at the particular moment in time represented by that point.
Study the Focus example and pay particular attention to steps 3 and 4. Complete the Focus Questions and continue to the next page for further commentary. If you would like to view more examples click here.
When completely satisfied you have an understanding of this topic move on to the activities section.
In Step 3 of the example, the points at t = 9 and t = 10 are chosen to draw a secant line and find its slope; Step 4 brings it closer by using t = 9.9 and t = 10 and repeats the process; if you want to be more accurate use t = 9.99 and t = 10 - check the calculation on your own. The closer the interval is to the required point the better approximation for the slope of the tangent at that point.
In general, for a point on this graph we could derive an expression for the slope of the tangent at any point. Let 
represent a point on the graph of 
or we can write the point as 
.
Choose a point very close to this point; h units away from it, which can be represented as 
. Use the slope formula and find an expression for the slope between these two points.
The slope of a tangent for this graph, in general, can be expressed as 
. As h becomes smaller and smaller (i.e. the points become very close that determines the secant line) the h gets closer and closer to the value of 0, and becomes negligible in the calculation. Therefore, the slope of the tangent can be represented as
The slope at x = 10 , then could be calculated from this expression as
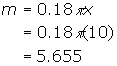
which is the value found in the example only more accurate. At 10 seconds, the area of the circle is increasing at the rate 5.655m2/sec
Note: The general form is very useful since the instantaneous rate can now be found for any time t in this function. For example at 3 seconds, the instantaneous rate is 
This procedure is applicable to any function by using 
and 
as two points. Use the slope formula and simplify to find an expression for slope; assume h is negligible since it so close to zero and generalize the slope for the tangent at any point which is the instantaneous rate of change at that point.
The instantaneous rate of change can be interpreted from the graph of a function. For example consider the following graph of a function and tangents at various points. Step through the example to observe the changes and then play it by using the show button to get a feel for how the slopes of the tangents are changing. Consider the questions that follow and answer each to your own satisfaction.
- What is happening to the slope as the curve rises?
- What is the slope at the vertex of the parabola?
- What is happening to the slope of the tangents as the curve falls?
- Interpret these results in terms of instantaneous rates of change at the various points.
Activity
Focus Questions p.89 - 90. Complete 9, 10, 11, 12, and 13
Think About p. 89, p.90(2 questions), p.91(2 questions), 92,, p.93 and p.94(2 questions)
Challenge Yourself p. 95
Check Your Understanding p.90 - 95. Complete 14 to 35 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
- A water cooler cup is in the shape of a right circular cone. Water is being poured into it at a constant rate. The height of the water t seconds after it is started to be filled is given by the formula
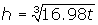. Find the rate at which the water level in the cup is rising 0.5 seconds after the start of the filling process.
Click here for suggested solution.
- A cube of ice has sides 5 cm on each edge. It is melting at the rate of 12mm/min for each edge. What is the average rate of volume decrease over the first 2 minutes? What is the instantaneous rate of decrease after 2 minutes?
Click here for suggested solution.
- A water cooler cup is a right circular cone with a height of 5 cm and a diameter of 3 cm. Water is running into the cup at 1.6 cm3/s. Find the rate at which the water level is rising when the water is 2 cm deep?
Click here for suggested solution.