Learning Resources

To find the average rate of change for volume decrease over the first two minutes you will require the initial volume and the volume at 2 minutes. The initial volume is 

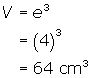
Since the rate of decrease is given in mm/min and the edge in centimetres, you must write the rate as 1.2 cm/min. In 2 minutes, an edge will decrease by 2 x 1.2 = 2.4 cm. The edge is now  4 - 2.4 = 1.6 cm. Therefore, its volume will be

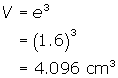
The average rate of change is the difference divided by the time

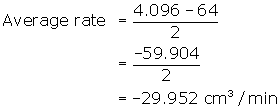
To find the instantaneous rate of change, you require a function describing the volume in terms of time. For t minutes an edge reduces by 1.2t cm. Therefore, after t minutes each edge will be (4 - 1.2t) cm in length. Using the formula for the volume of a cube, the function will be .

Average rate of change in volume compared to time is the slope of the secant line through  two points that are very close to t = 2 .

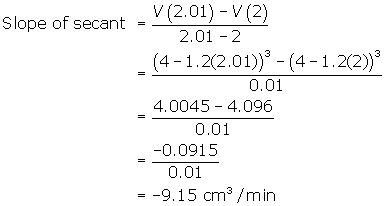
Since the points are very close together, we can use this as an approximation to the slope of the tangent at the point t = 2 which is the instantaneous rate of change at that point.

Therefore, the rate of change in volume at 2 minutes is approximately -9.15cm³/min.

Note each of the solutions are negative since the volume is decreasing.