Learning Resources

Since the problem requires us to find how fast the height (depth of water) is changing, we need to determine an expression or function for height in terms of time.

The water cooler cup can be represented as below:

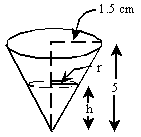
Note the relationship between the height and radius of the cone and the height and radius of the water can be represented by similar triangles.    

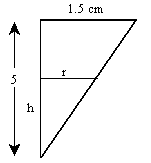
Using the fact that the sides of similar triangles are proportional, we have 

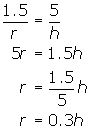
The water is pouring into the cup at the rate of 1.6 cm³/s. For any given time t the Volume is found by .

Since the problem requires us to find how fast the height (depth of water) is changing, we must determine an expression or function for height in terms of time.

Since the volume of a cone is given by , we can substitute 0.3h for r and obtain a formula for volume in terms of the height.

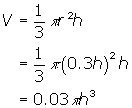
Solve for h since we require a function describing the height

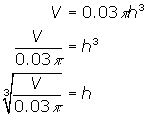
Using , the height in terms of time would be 

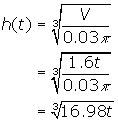
We can now calculate the volume for a height of 2 cm  and find the time at which it occurs and then use the h(t) to find the slope of a secant line very close to that time such that we can determine the instantaneous rate of change at that time. 

When h = 2, the radius is and the volume will be 

For , the time will be

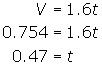
At 0.47 seconds the volume is 0.754 cm³ with a depth (height) of 2 cm. To determine the instantaneous rate of change the consider t = 0.48 and 
t = 0.47  and find the slope joining these two points on the function h(t).

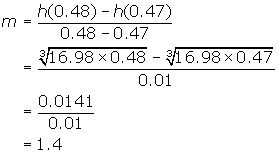
From this calculation we can deduce that the when the depth of the water is 2 cm, the height of the water in the cup is rising at a rate of approximately 1.4 cm/s