Learning Resources
Lesson
Read and complete Investigation 1 before continuing with this lesson.
The number pattern in this investigation is very easy to follow and you should be able to find it very quickly. It starts with a square composed of 4 rods, then for each extra square three rods are added since a common rod can be used to create the two squares. To solve the contractors problem, it is tedious to continue the pattern recursively for 63 sections. In Step E, find a "rule" to describe how to find the solution.
This investigation yields what we call in mathematics a sequence of numbers (see definitions in the side bar of your textbook). Each term is represented by the symbol 
and so on. A sequence is normally written in set notation and may be finite ( a set number of terms ) or infinite ( continues indefinitely ).
finite 
infinite 
Under Activities, complete investigation questions before continuing.
As you completed the Investigation Questions you encountered "sequence of differences". This is important since a "common difference" becomes the defining element of an arithmetic sequence. Investigation Question 6 is very important since it leads you to a generalization for the nth term of a sequence as tn . Be sure to complete this activity; seek help if necessary.
Note you should write the nth term both as a rule and in functional form for these questions and the Check Your Understanding exercises.
Consider the following example of a pattern:
Determine whether { 2, 6, 10, 14, ...} is arithmetic. If so, write the nth term both as a rule and in functional form.
Solution: To determine if the sequence is arithmetic, check to determine if there is a common difference. Click the Go forward one frame button to find the first three differences (you may use the other global buttons to navigate the window)
Since a common difference exist at the first level, we conclude that it is an arithmetic sequence
From the investigation questions we have an expression in functional form for the nth term as follows:
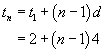
or this may be written as 
As a rule we write "the nth term is found by subtracting 2 from the positive multiples of 4"
The TI-83 graphic calculator can be used to generate a given arithmetic sequence by using the the recursive function. Click here to see a demonstration.
Activity
Generally, all questions will be assigned for you to complete; however, your teacher may assign only selected exercises. It is to your advantage to complete as many of these activities as possible to develop a greater understanding of the topics. Note that all investigation questions should be completed since many new ideas and concepts are developed in these problems.
Investigation Questions p.3 - 4. Complete all questions as indicated in the lesson
Challenge Yourself p. 4 and p. 6
Check Your Understanding p.4 - 6. Complete 7 to 16 inclusive.
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section for a quick quiz on this lesson.
Test Yourself
Write a Journal entry describing a procedure to determine whether or not a sequence is an arithmetic sequence. Explain why the slope in a linear function is equivalent to the common difference.
Answer each of the following questions:
1. If 
2. Using the function 
generate the first ten terms of the sequence . Graph the function. Find its slope and indicate what you notice.
3. If 
, devise a method to find an expression for tn . Use this expression to find t40 .
Click here to check your solutions. Be sure to close window when finished.