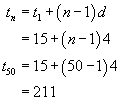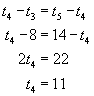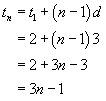Learning Resources
Home » » Courses » Mathematics » Advanced Mathematics 3205 (delisted) » Unit 01 » Set 01 ILO 01 » Solution
| 1. |
For the two terms given the difference is 4, therefore the general expression for an arithmetic expression containing these two terms will be
|
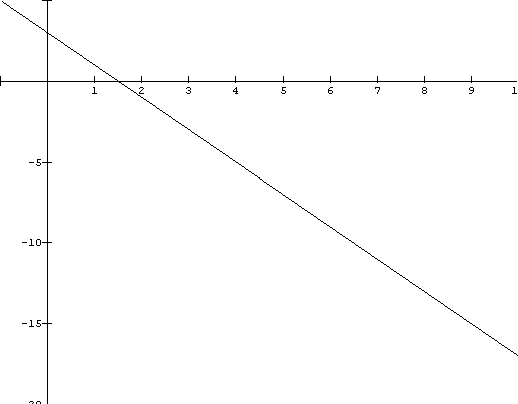
| 2. | Using the given function
 ,
we can substitute 1 to 10 inclusive into the function and calculate each
term or use the TI-83 calculator recursive function to find {1, -1, -3,
-5, -7, -9, -11, -13, -15, -17}.
Graphing the function we get
From the equation or the graph we see that the slope is -2, which is the same as the common difference for our arithmetic sequence. |
| 3. | A sequence is presented by
 .
We are given  .
Since an arithmetic sequence must have a common difference then we have
We now have the sequence
|
.
From these values we see that there is a common difference of 3, which
gives us term 1 and term 2 as 2 and 5 respectively. The general expression for an arithmetic expression containing these
terms will be