Learning Resources

Home »  » Courses » Mathematics » Advanced Mathematics 3207 (delisted) » Unit 03 » Set 07 ILO 04 » Go to Work

Lesson

You have worked with logarithms to many different bases. Focus M introduces a special type of logarithm called a "natural logarithm." This is a logarithm to base e. For convenience, instead of writing , the natural logarithm of x is denoted ln x. 

Common logarithms, you will recall, are logarithms to base 10. For convenience, "10" is not written in as the base. Rather, it is understood that the base is indeed 10. Similarly, when you see ln x, it is understood that the base is the number e.

You will find a natural logarithm button on your calculator. Locate this LN key. It can be used to calculate the natural logarithms of applicable numbers.

To evaluate ln 3, simply press LN, followed by the number 3. When you are evaluating ln 3, you are actually evaluating .  

In essence, you are trying to determine the power to which e should be raised to produce an answer of 3. Knowing that e has a value of approximately 2.7183, can help you get a rough estimate of the solution before using the calculator.

The domain and range of y = ln x is the same as the domain and range of . Record the domain and range of y = ln x in your notebook. You may verify your results.

The properties of logarithms studied in Mathematical Modeling, Book 3 also hold true for natural logarithms. A review of the basic properties is provided for those of you who cannot remember the rules.

Before beginning the Focus, answer the questions below for practice with the properties of logarithms. Remember, lnx is a logarithm to base e.

  1. Write ln 4 1.4 in exponential form.
  2. Write ln 20 - ln 2 + ln 5 as a single logarithm.
  3. Write 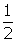ln 36 as a single logarithm.
  4. Solve for x: ln x = 14.
  5. Evaluate ln 1.
  6. Evaluate ln e.

Once you have completed the task, you may check your solutions.

Do you recall how to solve exponential equations in which like bases cannot be found?

Consider the equation 4x = 15. You should have an approximate answer for x in mind. Solve this equation. Once you have recorded your solution, check the result.

It is by this same process that you will solve an exponential equation involving base e. When taking the logarithm of each side of the equation, do you think you will use common logarithms as before? Why or why not? If common logarithms are not used, what type of logarithm will be used?

Consider ex = 18. Can you mentally determine an approximate value for x? Solve the equation to verify your thoughts. You may check your solution.

Read Focus M on page 189 of your text and answer the Focus Questions.

An example is provided below.

Activity

Focus Questions page 189 #'s 27 & 28

C.Y.U. pages 190 - 192 #'s 29 - 39

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

  1. What is the inverse of f(x) = ln x?
  2. Solve for x: ln x = 7.
  3. Solve for x: 12e-x = 6.
  4. Solve for x: e2x - 5ex + 6 = 0.

Solutions

  1. f -1(x) = ex
  2. x = e7 or 1096.633158
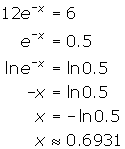
  4. The given equation has a quadratic form and can be factored.