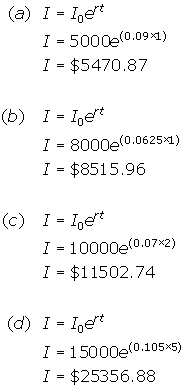Learning Resources

Home »  » Courses » Mathematics » Advanced Mathematics 3207 (delisted) » Unit 03 » Set 07 ILO 03 » Go to Work

Lesson

Investigation 9

This investigation should enable you to gain some familiarity with the behaviour of the function, y = e^x.  You will examine exponential growth and decay, and compare these functions with y = e^x.

Follow the Procedure as outlined on page 186 of your text. Hints and suggestions are available for various steps, should you experience difficulty.

• Step A
• Step C
• Step D
• Step E

Answer the Investigation Questions.

Investigation 10

In the previous Investigation you discovered that the value of the derivative of 
f(x) = e^x at x = 0 is 1. Now you will determine the derivative of f(x) = e^x at any value of x. The definition of the derivative will be used to develop an answer.

Do you know why the Power Rule cannot be used to find the derivative of 
y = e^x? Record your answer and then check to see if you are correct. 

Proceed with the Investigation as outlined on page 187 of your text. Some hints and suggestions are offered for various steps, to be used only as needed. 

• Step A
• Step B
• Step C
• Step D

Answer Investigation Question #14.

A summary of the Investigation is provided.

Notebook Entry: Record the derivative of f(x) = e^x .

An example is provided below.

Activity

C.Y.U. pages 187 -189 #'s 15 - 26

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

1. If you graphed y = 4^x, y = 10^x and y = 7^x, which one would be sandwiched between the other two?
2. Does the function y = 4^x represent exponential growth or decay?
3. Does the function y = 5^-x represent exponential growth or decay?
4. Use a formula to calculate the value of each investment described below, assuming continuous interest.
   (a) $5 000 at 9% for one year
   (b) $8 000 at 6.25% for one year
   (c) $10 000 at 7% for two years
   (d) $15 000 at 10.5% for five years

Solutions

1. The graph oh y = 7^x would be sandwiched between the other two graphs.

2. Exponential growth

3. Exponential decay

4.