Learning Resources

Investigation 9: Looking Inside the Box: Properties of the Function y = ex & Investigation 10: The Derivative of y = ex

Step D

• You are to estimate the slope of the tangent to the graph at x = 0 by calculating the slopes of various secants to the graph for which one intersection point is (0, 1). 
• For example, you can find the slope of the secant containing the points 
  (0, 1) and (0.5, f (o.5)), which is the point (0.5, 1.649). 
• You might also find the slope of the secant containing the points (0, 1) and (0.1, f (0.1)), which is the point (0.1, 1.105). 
• Perform similar calculations with the x-coordinate of the second point becoming close to zero. 
• You should observe that as the second point you choose gets closer and closer to the point (0, 1), the slope of the secant gets closer and closer to one. 
• Find an expression for the slope of the secant line through the points (0, 1) and (h, e^h ). 
• The resulting expression, you can conclude, also gets closer and closer to one, as h tends to zero. Essentially, this means that as the value of h tends to zero, the expression 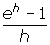approaches 1. 
• The end value of this limiting process is one. This is, of course, the value of the derivative of the function y=e^xat the point (0, 1).