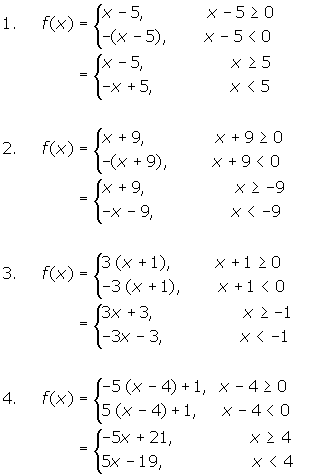Learning Resources
Lesson
The absolute value of a number x, denoted 
, refers to the distance from x to zero. Thus, absolute values are never negative. Below is the standard definition for the absolute value of x.
For any real number, x: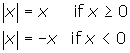 
No doubt, when looking at the second part of the definition, some of you are thinking, "How can this be if absolute values are always positive?"
Upon close examination of the definition, however, you will realize that it does not imply that taking the absolute value of a number gives a negative result. Rather, it states that the absolute value of a non-negative number is that number itself. Whereas, the absolute value of a negative number is its additive inverse.
You will all agree, for example, that |3| is indeed 3. What about |-3|? This too has a value of 3. In other words, |-3| = -(-3) = 3. The answer is actually the additive inverse of -3. It is this concept that the second part of the definition illustrates.
Below is the graph of f(x) = .
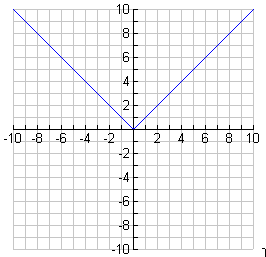
Clearly, f(0) = 0. Thus, the function is defined at x = 0. Suppose you were asked to draw a tangent line at the point (0,0). Is there more that one possible tangent? What does this imply about the derivative at the point (0, 0)? You may check your responses.
We will use the definition of a derivative to calculate the derivative of the function f(x) = at the point (0, 0).
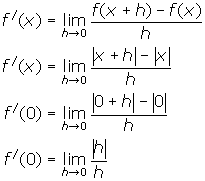
Since direct substitution is not possible, the right and left hand limits must be evaluated. Set up tables of values to assist you in this process. Record your conclusion. Once this task is completed, you may verify your result.
It should come as no surprise that the function f(x) = has no derivative at
x = 0, since there were many possible tangents at this point. Since the tangent line is not unique, the derivative too is not unique.
The absolute-value function, you have discovered, is defined differently for x < 0 than it is for x > 0. Since the function is defined differently over two intervals, it is considered a piece-wise function and can be written as shown below.
You are now ready to proceed with Focus J and the Focus Questions on page 168 of your text.
Activity
Focus Questions page 168 #'s 1 & 2
C.Y.U. page 168 #'s 3 & 4
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
Each function below can be considered to be a piece-wise function defined separately over two intervals. Write a piece-wise definition for each function.
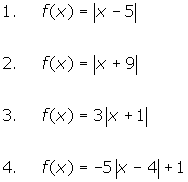
Solutions
