Learning Resources
Lesson
You will get a break from working with rational expressions as this Focus concentrates on solving rational equations. "What's the difference?" some of you may be wondering.
A rational expression is simply that; an expression. A rational equation, however, is an equation that contains rational expressions. An equation must contain expressions on two sides of an equal sign. Expressions are to be simplified, whereas equations are to be solved for a given variable.
Take, for example, 
+ 
x.
This is a rational expression, whereas + x = 4 is a rational equation.
In the first situation, you cannot solve for x since you do not know what the expression is equal to. You cannot assume it is equal to zero! The second scenario, however, indicates that the expression is equal to 4. Thus, you can solve the equation for x.
No doubt you have realized by now that your work with rational expressions in the previous lesson will be invaluable to you. The skills acquired in working with rational expressions will facilitate the simplification and solution of rational equations. At first, however, you will use graphical methods to solve the equations.
Before examining the examples given in the Focus, you first of all need to familiarize yourself with the procedure of solving rational equations. Remember, the goal is to get rid of the existing fractions, creating a much simpler equation to solve. You may need to refer to the previous page to have a second look at the two common procedures in which to accomplish this.
For each equation below, identify whether it would be beneficial to cross multiply or multiply each term by the L.C.D. to get rid of existing fractions.
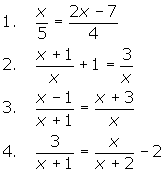
Once you have recorded your answers, you may check your solutions.
Now that you are aware of which procedure to use in each case, solve each of the above four equations for x. Be sure to list any restrictions on the domain, as you will have to reject that particular solution should it be one of the values for x. It might be wise to list the restrictions in the first step so as not to forget about them.
Once you have the problems solved, you may view a detailed solution of each.
Some of the work in this lesson involves setting up and solving word problems. Correctly creating a valid equation to represent the given information is the most important step in the process of working with equations. Keep in mind that such equations are usually based on rates and proportions.
Here is a general strategy for solving applied word problems:
- Read the problem carefully. Give the problem some serious thought, and perhaps reason out some possible solutions. Sometimes, this can enable you to solve the problem.
- Translate the problem into mathematical language. Usually this involves assigning variables to unknowns and creating an equation. At times, drawing a diagram or chart may help.
- Solve the equation and check to see if the solutions of the equation are acceptable in the context of the problem.
Read through examples 5 and 6 on pages 147 to 149 of your text and answer the Focus Questions.
An example is provided below.
Activity
Focus Questions page 149 #'s 16 & 17
C.Y.U. pages 149 - 151 #'s 18 - 24
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
-
The following questions are based on the rational equation below. By what expression would you multiply each term to eliminate the fractions? What values of x must be restricted from the domain of the function? Solve the equation.
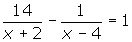
- Set up an an equation to represent each word problem below. Do not solve your equations.
- (a) A boat travels 246 km downstream in the same time that it takes to travel 180 km upstream. The speed of the current in the stream is 5.5 km/hr. Find the speed of the boat in still water.
- (b) Bill can do a certain job in 4 hours. Jim can do the same job in 3 hours. How long will it take both of them working together to do the same job?
Solutions
1.
- Multiply each term by the L.C.D. which is (x + 2)(x - 4).
- The restrictions are x
-2,4 - The solution is provided below.
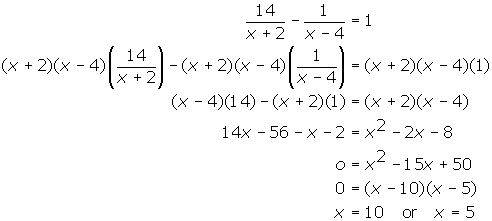
2. (a)
- Let x represent the speed of the boat in still water.
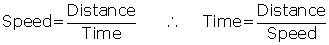
| Speed | Time | |
| Downstream | Speed of boat + speed of current x + 5.5 |
 |
| Upstream | Speed of boat - speed of current x - 5.5 |
 |
Since it is given that the times are equal, the desired equation is :
2. (b)
- It is important to note that if a job can be done in time t, then
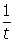of the job
can be done in 1 unit of time. - Bill can do the job in 4 hours. Thus he can do
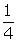of it in 1 hour. - Jim does the job in 3 hours. Thus he can do 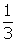of it in 1 hour.
- Together they can do 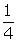+ 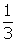of it in 1 hour.
- Thus, the desired equation is + = .
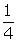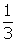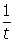