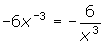Learning Resources
Lesson
By now you have realized just how tedious and time consuming finding the derivative can be at times. You will be happy to know that the purpose of this Investigation is to find an alternate method to determine the slope of the tangent to the graph of a polynomial function at an established point.
Your task is to use the limit definition of the derivative to differentiate given polynomial expressions. It will be helpful to refer to previously completed questions looking for patterns as you complete the required charts.
Complete the Investigation as outlined on pages 98 & 99 of your text. As well, answer its related questions. If time is a factor, your on-line teacher may agree to allow you to work in pairs when completing the tables. Hints are provided for selected steps of the Investigation. Do not avail of them unless you are experiencing difficulty.
Notebook Entry: Record the Power Rule and an example of how it works.
For practice, you should use the notations y /, f /(x) and 
interchangeably to represent the derivative.
Activity
C.Y.U. page 100 #'s 19 -22
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
Find y / for each of the following.
- y = x10
- y = 6x4
- y = -3x7 + 2x
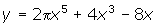
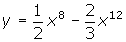
- y = (x + 3)(x - 4)
- y = 3x-2
Solutions
- y / = 10x9
- y / = 24x3
- y / = -21x6 + 2
- 4. y / = 10
x4 + 12x2 - 8 - y / = 4x7 - 8x11
- Foil the expression out first before finding the derivative. y / = 2x - 1.
- y / =
