
Learning Resources
Lesson
Before beginning the Investigation, it is necessary to establish the difference between an average rate of change and an instantaneous rate of change.
Consider velocity, for example. A car travels 210 km in two hours. Thus its average speed, or velocity, is ![]() , or 105 km/hr.
, or 105 km/hr.
This is the average rate of change of distance with respect to time. However, at various times throughout the trip, the speedometer did not read 105 km/hr. Thus, we say that the average speed is 105 km/hr. A snapshot of the speedometer taken at any instant would indicate the instantaneous speed, or rate of change.
As you can see, an average rate of change is taken over a set period of time, while the instantaneous rate of change is taken at a particular moment in time.
The purpose of Investigation 7 is to estimate the instantaneous rate of change at a point on a distance-time graph. With your on-site teacher's permission, you may work in pairs or small groups to complete this activity. Each one of you, however, must record the information in your own notebook, as it is crucial for your understanding of the outcome of the Investigation.
Some of you may need to be reminded that velocity is a vector quantity. A positive velocity means that the projectile is moving away from the starting point. A negative velocity means that it is coming back toward the starting point.
Read the introduction to the Investigation on page 89 of your text. Do not proceed any further until you have completed the assigned reading.
Why is the velocity of the soccer ball zero when it has reached its maximum height? Record your answer. Verify your answer.
Carry out the procedure for the Investigation. Be sure to complete both charts in your notebook.For Step A, you may use either the given graph of the function or the polynomial equation for the function to assist you in completing the table. As well, you can use the TABLE feature on your graphing calculator. To do so, enter the times in Lists 1 and 3, and enter the appropriate functions in Lists 2, 4, and 5. After completing the Investigation and the related questions, make the following notebook entry.
Notebook Entry: Record why it is obvious that the the velocity approaches 0 m/s as the time gets closer to 1 second from the left side of the graph as well.
Focus F: Limit Notation
In Chapter 1 of this course, you were introduced to the concept of a limit of f(x) as x approaches infinity. This Focus introduces the concept of a limit of f(x) as x approaches a finite value. Although you will proceed through the activity with relative ease, it is crucial that you, in the end, have a solid understanding of the concept of a limit, as well as the notation. You will encounter this topic again in Chapter 3.
Carefully read the Focus as described on pages 91& 92 of your text. Answer the Focus Questions on page 93.
If needed, you may view a summary of points from the Focus.
Activity
Focus Questions page 93 #'s 4 & 5
C.Y.U. pages 93 & 94 #'s 6 - 10
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
1. A projectile is fired upward from the top of an 80 m building so that its height,
in meters, above the ground t seconds later is h(t) = 80 + 64t - 4.9t2.
Find the average velocity over the interval from t = 0 to t = 3.
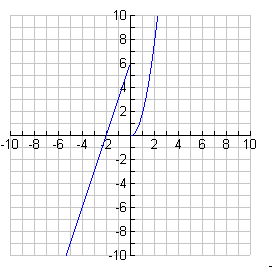
2. Using the graph of f(x) below, evaluate each of the following limits.![]()
Solutions
1.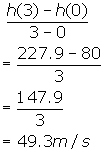
2. 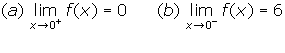
(c) The right and left hand limits of f(x) are as x approaches 0 are not the
same finite value. Hence, the limit of f(x) as x approaches 0 does not
exist.