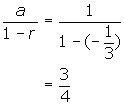Learning Resources
Lesson
Investigation 5: An Amazing Shape
In this investigation you will see the concept of fractals to explore the formula to sum an infinite geometric series.
Examine the first two drawings given in the introduction of Investigation 5 on page 32.
Similar figures, you may recall, have the same shape but not the same size. The figures in this Investigation are said to be self-similar since the pieces are all similar to the overall shape. Draw, in your notebook, a self-similar figure. The choices are many. You may, for example, draw a parallelogram made up of smaller parallelograms similar to it.
Read the remaining part of the Investigation. Do not begin the Procedure, and do not proceed any further on this web page until you have completed this assigned reading.
The notion of fractal involves self-similar shapes that are irregular or fragmented. A fragmented shape is one that is made up of many little pieces rather than a few straight lines. The Koch snowflake is such an example. The animation below will demonstrate the creation of its design.
Focus E: Converging and Diverging Series
Examine closely the sequence 
before answering thequestions below.
- Write a formula for this sequence of terms.
- What type of sequence is it?
- Does it converge or diverge?
Once you have recorded your answers, you may verify them.
Since the above series is infinite, it is physically impossible for you to add up all terms. In other words, you cannot sum the entire series. You can, however, create partial sums.
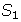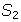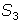- Find
, 
, 
and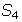 
. - What do you notice about these partial sums? Do they converge?
- Find a formula for the
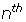partial sum,
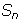. What isits limit?
Once you have recorded your answers, you may view the solutions.
Since there is a limit, that limit is defined as a sum of the series. You can, therefore, write 
. This means that if we continue to find the partial sums of the given sequence, the results will get closer and closer to 1.
Consider now the sequence {2, 4, 8, 16, 32, ...}.
- Write a formula to represent the sequence.
- What type of sequence is it?
- Does it converge?
Once the task is completed, verify your solutions.
Find the first four partial sums. Is there a limit here?
You are now ready to begin the Focus Questions on page 34 of your text.
After you have completed all Focus Questions, you may view a summary of the Focus.
An example is done below.
Notebook Entry: Record the formula for summing a convergent infinite geometric series.
Note: You will need graph paper for the next lesson. Be sure to have some on hand before attempting the next Investigation.
Activity
Focus Questions page 34 #'s 25 & 26
C.Y.U. page 34 - 36 #'s 27 - 35
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
Examine each infinite geometric series below. Find the first four partial sums.
Also find the sum of the series if it converges.
Solutions
1. (a)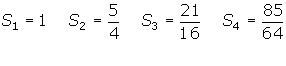 
This is an infinite geometric series in which r = 
. It converges to the sum
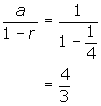
(b) 
This is an infinite geometric series in which r = 
. It converges to the
sum 