Learning Resources

Investigation 5: An Amazing Shape & Focus E: Converging and Diverging Series

• Notice in Focus Question 26(a) the series is finite, whereas the one given in part (b) is infinite. 
• The formula for the sum of a geometric series is .
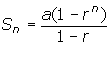• However, if the geometric series in infinite and the common ratio is between -1 and 1, the series will converge to the sum . 
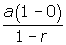• The reason for this has to do with the fact that if -1 < r < 1, then r ⁿ gets closer and closer to zero, as n gets larger and larger.
•  Thus, you are left with the formula 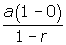which is obviously .
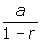• If the common ratio, r, is not between -1 and 1, then the infinite geometric series will diverge.