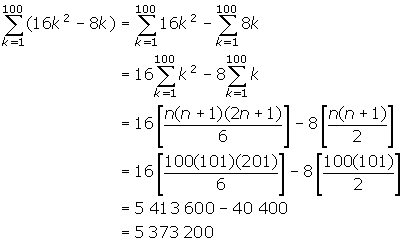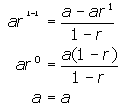Learning Resources
Lesson
Think about situations in which you have been asked to prove something. Generate a list of examples and recall the methods you have used to substantiate your proof.Later, you will classify these examples as inductive or deductive.
Examine closely the statements below:
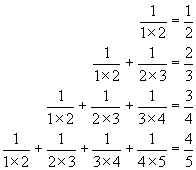
Do you know what the next statement would be? Record your answer.
You have probably realized by now that there is indeed a pattern here. It would seem that the following statement holds true:
Although you may have convinced yourself by now that this statement is definitely true, simply checking a few values for patterns does not constitute a proof. Just because you can show something is true say four or five times, does not mean it must always be true. In order for one to accept this statement as true, it must be shown that it holds true for all natural numbers. One method of doing this is by using a process called mathematical induction.
Before beginning the process of mathematical induction, it is important that you understand the set of natural numbers, or the counting numbers, to which they are commonly referred. Essentially, they are numbers contained in the set represented by N = {1, 2, 3, 4, 5, ... }. Note that the first natural number is one.
This Focus provides a technique for proving something is true for all natural numbers without having to perform the impossible task of checking every one of them. The principle of mathematical induction is based on the notion that if a statement is true for a particular natural number value and, if you can prove that whenever it is true for one value, it is true for the next, then the "domino effect" would suggest it be true for all natural numbers greater than the original one for which the statement is verified.
One way to illustrate the principal of mathematical induction is to consider a row of dominoes, infinite in number, labeled 1, 2, 3, ..., n, .... Each domino is initially standing up.
Let P(n) be the proposition that domino n is knocked over. If the first domino is knocked over - i.e., if P(1) is true, and if, whenever the nth domino is knocked over, it also knocks the (n + 1)th domino over - i.e., if P(n) causes P(n + 1) to be true - then all the dominoes are knocked over.
Another way to illustrate the principal of mathematical induction is to consider an infinite number of people in a lineup spreading a secret. The people are labeled Person 1, Person 2, Person 3, ..., Person n, ...
Let P(n) be the proposition that Person n learns the secret. If Person 1 learns the secret - i.e., if
P(1) is true, and if, whenever the nth person learns the secret, if also shares the secret with the (n + 1)th person - i.e., P(n) causes P(n + 1) to be true - then everybody learns the secret.
Read the definitions of deduction and induction provided on the left hand side of page 22 of your text. Also read the first part of Focus D on page 22 of yourtext.Do not read beyond page 22 until you are instructed to do so.
In a nutshell, deductive proof involves going from general to specific. We accept the truth of a general statement and later, when faced with a particular example of the general case, we deduce it to be true as well. Inductive reasoning, however, goes from the specific case to general principles. When we make a general statement from a number of particular examples, we are thinking inductively. Check your knowledge of these two concepts by answering the questions below.
Classify each of the following examples as either deductive or inductive reasoning:
- All pencils contain graphite. You own a pencil. Thus, your pencil contains graphite.
- The sum of the interior angles of a triangle is (3 - 2) x 180°. The sum of the interior angles of a quadrilateral is (4 - 2) x 180°. Thus, the sum of the interior angles of an n-sided convex polygon is (n - 2) x 180°.
- All dogs are animals. Rover is a dog. Thus, Rover is an animal.
- The hockey team scored 2 goals in the third period of each game of the season. Thus, they will score 2 goals in the third period of the last game of the season.
Click here to check your answers.
Read the next part of the Focus, beginning on page 23, up to and including example 1. Do not read example 2 at this point.
Explore morecases of Cain's observation, such as the value of 35 - 1, 36 - 1 and 37 -1. Suppose you did 20 more examples of this conjecture, would this beenough to prove it?
Cain's conjecture is provable by the process of mathematical induction. There are 4 essential steps to the procedure. A detailed explanation of each of the four steps is offered if you are having difficulty interpreting the information provided in the textbook.
Read through example 2 on pages 24 & 25 of your text. Some hints to help you understand certain procedures are available. Use them only if you are experiencing difficulty.
Note that when proving by mathematical induction, it is not necessary to organize the steps in statement and reason form. The text has only done this in an attempt to demonstrate the logistics behind each step. You, however, may simply organize the workings used in step 3 in a logical algebraic manner, as an alternative to this approach if you wish.
Four additional examples are provided if you feel the need for more practice before moving on to the Focus Questions.
Example 1
Prove that 
Solution.
Step 1: Prove the statement true for n = 1.
Therefore, the statement is true for n = 1.
Step 2: Assume the statement is true for n = k.
Assume that
.
Note: Look for the similarly colored parts of the equation in step 3.
Step 3: Prove the statement true for n = k + 1. In other words, prove that
.
The procedure should be as follows:
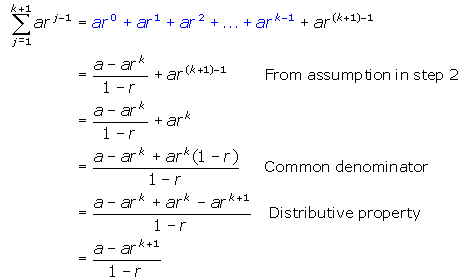
Thus, the statement is proved true for n = k + 1 if it is assumed true for n = k.
Step 4: Write a conclusion.
Based on the principle of mathematical induction, it is true that for all natural numbers, n.
Example 2
Prove that if n is a natural number, 3 is a factor of n3 - n + 3.
Solution.
Step 1: Prove the statement true for n = 1.
(1)3 - 1 + 3 = 3, and 3 is a factor of 3.
Step 2: Assume the statement is true for n = k.
- Assume that 3 is a factor of k3 - k + 3. This, in turn, means that k3 - k + 3 is a multiple of 3. Hence, k3 - k + 3 = 3m.
- Using the notation3m is a way of describing the fact that the expression is a multiple of3.
- Keep in mind that if, during the completion of step 3, you see the expression k3- k + 3, you can replace it with 3m.
-
A good strategy then, would be to try and get this expression in step 3. Look for the color coded expression.
Step 3: Prove the statement true for n = k + 1. i.e. prove (k + 1)3 - (k + 1) + 3 is a multiple of 3.
(k + 1)3 - (k + 1) + 3 = (k3+ 3k2 + 3k +1) - k - 1 + 3 Expansion of (k + 1)3
= (k3 - k + 3) + 3k2 + 3k
= 3m + 3k2 + 3k From the assumption in step 2
= 3(m + k2 +k) This is a multiple of 3
We have proved the statement true for n = k + 1, assuming its truth for n = k.
Step 4: Write a conclusion.
Based on the principle of mathematical induction, it is true that if n is a natural number, 3 is a factor of n3 - n + 3 for all natural numbers, n.
Example 3
Let's return to the example given at the beginning of this lesson. Recall that:
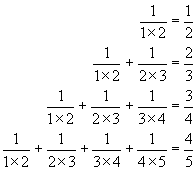
which suggests the formula 
. Below is a proof of this by Mathematical Induction.
Example 4
The following is a useful formula that you may need in the next section.
Notebook Entry:Record definitions of the following:
- deduction
- induction
- the principle of mathematical induction
The Principle of Mathematical Induction has been used in recreational mathematics as well. For an example, click here.
Activity
Focus Questions page 26 #'s 1 - 4
C.Y.U. page 26 - 27 #'s 5 - 7
Note: Question #6 is very important as these formulas come up again later. Be sure you know how to use the formulas. Read the note in the margin on page 26 of your text.
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
Classify each of the following as deductive or inductive reasoning.
(a) Butter melts when heated. If Jan heats the butter, it will melt.
(b) John always gives Sue a box of chocolates for Valentine's Day. Thus, on February 14th of this year, Sue will get a box of chocolates from John.
2. Use the formulas from question #6 on page 26 of your text to evaluate
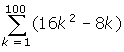
Solutions
1. (a) deductive
(b) inductive (a general statement is made based on a number of particular examples)
2. First of all, manipulate the given expression to create 2 summations. Then factor any existing scalars out of each sigma notation. Finally, use the appropriate formulas to sum each series.
