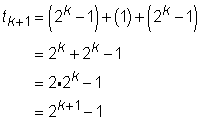Learning Resources
Proof by Induction
The Tower of Hanoi
The Tower of Hanoi is a famous puzzle (a version of it was even used on Survivor Thailand as an immunity challenge). There are three poles. A set of disks of different sizes are placed on one pole, with the largest disk on the bottom and the smallest disk on the top. The object of the puzzle is to move all of the disks from pole to another pole without ever placing a larger disk on a smaller disk. Disks can only be moved one at a time, and one pole can be used for storage.
Can you solve the Tower of Hanoi puzzle for three disks? Click on the Start button and try it, and record how many moves it takes you!
Did you finish the puzzle? If so, did you complete it in the minimum number of moves? To check, click here to use the Tower of Hanoi solver.
Once you have the idea of the puzzle, try to solve it for 4 and 5 disks. You can always check your answer using the solver.
You may be asking, 'What does all of this have to do with Mathematical Induction?" We're getting to that! We are going to develop a formula that will relate the number of disks to the minimum number of moves, and then we are going to show this formula is true by Mathematical Induction.
Using the Tower of Hanoi solver, you should be able to verify the following table:
| Number of disks (n) | Minimum Number of Moves (tn) |
| 1 | 1 |
| 2 | 3 |
| 3 | 7 |
| 4 | 17 |
| 5 | 31 |
It appears that![]() . Let's prove this by Mathematical Induction.
. Let's prove this by Mathematical Induction.
Prove that the minimum number of moves it will take to solve the Tower of Hanoi puzzle with n disks is ![]() .
.
Step 1: Show the statement is true for n = 1.
We know that if we have 1 disk, it only takes 1 move to transfer the single disk to another pole. Since ![]() , the statement is true for n = 1.
, the statement is true for n = 1.
Step 2: Assume the statement is true for n = k.
That is, assume for k disks, it will take ![]() moves.
moves.
Step 3: Show that the statement is true for n = k+1
We want to show that ![]()
Consider the situation where we have k+1 disks. By Step 2, we know it will take ![]() moves to move the first k pieces to another pole. Then, we take 1 move to transfer the k+1 disk to a new pole. Finally, we have to move the k disks back onto the k+1 disk, which will take
moves to move the first k pieces to another pole. Then, we take 1 move to transfer the k+1 disk to a new pole. Finally, we have to move the k disks back onto the k+1 disk, which will take ![]() moves. Adding the total number of moves together we get:
moves. Adding the total number of moves together we get:
Thus, by the Principle of Mathematical Induction, the minimum number of moves it will take to solve the Tower of Hanoi puzzle for n disks is ![]() .
.