
Learning Resources
Lesson
In this investigation, you will have to use your skill of shrinking and stretching graphs to explore the equation of an ellipse and how it is similar to and different from a circle.
For this investigation you will require
- compasses
- rulers
- graph paper
For Step A and Step B, the unit circle is stretched in only one direction - horizontally. Recall that the coefficient ½ causes the x-co-ordinates to double, stretching the circle horizontally by a factor of 2. Step C requires you to read the intercepts from your graph and verify that these points satisfy the equation by substitution.
Step D and Step E repeats the earlier steps by stretching vertically. Again recall that the coefficient ![]() causes the y co-ordinate to triple, stretching the circle vertically by a factor of 3.
causes the y co-ordinate to triple, stretching the circle vertically by a factor of 3.
In Step F, combine the horizontal stretch and vertical stretch and compare it to the unit circle. Write the mapping that depicts this transformation keeping in mind the stretch factors for each direction. You should be able to graph the equation in Step G without drawing the unit circle first. Use the stretch factors to find the new intercepts and sketch the graph.
In the next three steps, you will have to examine the similarities and differences between circles and ellipses. You will note that the length of the axes is double the factor the circle has been stretched in that direction ( or ![]() )
)
Step K and Step L will provide practice for you in graphing an ellipse that is centred on the origin.
In Step M the ellipse is moved of the origin by using an horizontal and vertical translation. Remember to write it as a mapping when completed.
We are again going to consider the transformation of the unit circle which has equation x2 + y2 = 1. In the last lesson, the stretch in both the horizontal and vertical direction was the same, thus preserving the circular shape. In this lesson, we will explore stretching by a different factor in the two directions. The figure thus obtained is called an ellipse. The diagrams below show ellipses formed by this type of transformation.
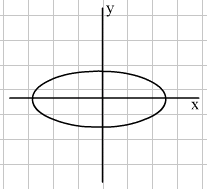
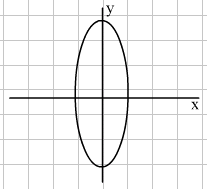
Greater horizontal stretch Greater vertical stretch
The rules for the transformational form are still the same. Multiplying the x value by a factor stretches horizontally, multiplying the y value by a factor stretches vertically. Click the Go forward one frame global button and click on any of the show buttons to see the transformation corresponding to the equation. Record in your note books the equation and draw a sketch of it for future reference. Pay particular attention to the size and direction of the stretch and the coefficients of the variables.
The figure produce by stretching a circle by different factors horizontally and vertically is called an ellipse. An ellipse does not have a diameter since its width varies with the direction. It does have two axes: a major axis and a minor axis, the length of which are determined by the stretch factor. The major axis is the longer axis and the minor axis is the shorter one. This is indicated in the diagram below:
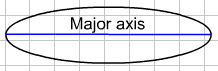

Go back to the transformations above and for each of them record in you note book, next to the equations and graphs you have already sketched, the length of the major and minor axes and then compare them to the coefficients of the variables. Make a conjecture about the relationship between the length of the axes and the coefficients of the squared terms? Click here to see if your conjecture is correct.
Using the major and minor axes is a quick way to sketch the graph of an ellipse. If you draw these axes first, it provides a framework on which to sketch the graph.
The point of intersection of the major and minor axes is the centre of the ellipse:
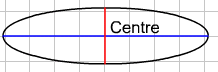
In all the transformations shown above, only a stretch was involved. The unit circle was not translated before the stretch and hence the centre of the ellipse remained at the origin. If a translation is also involved, you can either translate first and then do the stretch, or do the stretch first and then translate.
Example
Sketch the graph of ![]()
Solution
The centre of the ellipse is at ( 3 , -1 ) with a horizontal stretch of 3 and a vertical stretch of 5. The length of the minor axis is 6 and the length of the major axis is 10. The method used is to first translate the unit circle in order to locate the new centre of the ellipse. The stretch is then applied to the diameter by drawing the major and minor axes. And finally, the ellipse is sketched around these axes. This process is shown in the following interactive window; go forward one frame and click on show to see the ellipse graphed; click on Go to beginning at the end of the graphing:
If the equation of the ellipse is in transformational form, it is relatively easy to sketch its graph using the above method. However, most often the equation is not in transformational form and so it has to be rearranged first before this method can be used. Some examples of how to rearrange an equation to put it in transformation form are shown below.
Example 1
Write the following equation in transformational form: 25x2 + 4y2 = 100.
Solution
Follow the steps in the interactive window below to view this conversion.
Example 2
Write the following equation in transformational form:
9x2 + 4y2 + 18x - 32y + 37 = 0
Solution
Follow the steps in the interactive window below to view this conversion.
You should now be ready to do the work assigned for this lesson.
Activity
Investigation Questions p.265 - 266. Complete 42, 43, 44, 45, 46 and 47
Check Your Understanding p.266 - 267. Complete 48, 49, 50 and 51
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
Rewrite each of the following equations in transformational form. State the centre. Determine whether the graph is a circle or an ellipse. If it is a circle, state the radius. If it is an ellipse, state the length of the major and minor axes. Graph each equation.
Click here for suggested solution.