Learning Resources
Lesson
In this investigation you will discover a relationship between the sum and product of the roots of a quadratic equation and its coefficients.
Step A
Find the solutions by using any one of the methods learned to date for solving quadratic equations. You require the roots before you can compare the sum and products of the roots to the coefficients.
Note that the patterns discovered in the investigation applies to a = 1 for the quadratic equation. In the investigation questions, you will deal with the situation where a is any value other that zero.
Step B
Simply find the sum of the roots for each equation in Step A and the product of the roots for each equation in Step A.
Step C
Compare your answers in Step A and Step B, the pattern should be obvious.
Carry out the investigation and complete the investigation questions before continuing.
In this investigation the sum and product of the roots for a quadratic equation were found and compared to the coefficients of the equation. If 
represent the two roots then the following results occurred;
for the quadratic equation 
when a = 1.
This is very useful since if the roots of an equation are given, the equation can be very easily found by using the form
or the x-intercepts will give the equation of the function as
When a has a value other than one and not zero the relationship is
Make note of these conclusions !
Activity
Investigation Questions p.58 . Complete 65, 66 and 67
Think About p.58
Challenge Yourself p.59
Check Your Understanding p.59 - 60. Complete 68, 69, 70, 71 and 72
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
- Find the sum and the product for the roots of the equation
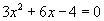without solving the equation. - Check that
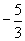and 1 are roots of the equation 
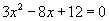. - Find the quadratic equation with roots which are the squares of the roots of
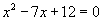
Check your solutions!