Learning Resources

1. Find the sum and the product for the roots of the equation without solving the equation.

Solution

For a quadratic equation of the form the sum of the roots and product of the roots are given by where represent the roots of the equation. For the above equation, a = 3,  
b = 6 and c = -4; therefore

• the sum of the roots is

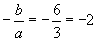
• the product of the roots is

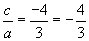
2. Check that and 1 are roots of the equation .

Solution

For this equation a = 3, b = -8 and c = 12.

Compare the sum and product of the suggested roots with the sum and product of the roots of the equation

• Sum: 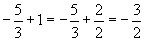and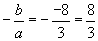

Since the sum of the suggested roots is different than the sum of the roots as determined by formula, then these are NOT the roots of the equation.

3. Find the quadratic equation with roots which are the squares of the roots of

Solution

Since the roots of a quadratic equation of the form is  where are the roots, we note from the equation we want two numbers with a product of 12 and a sum of -(-7) or 7 which means the roots are 4 and 3 (Note: you cold find these roots by solving the equation by any of the methods studied in this unit.). Therefore, the squares of the roots are 16 and 9. The equation that has these as roots will have a sum of roots 25 and a product of roots 144. This gives the following equation: