
Learning Resources
Lesson
In this lesson we are going to explore experimental probability by performing simulations to model some situations. A simulation is a model that is usually simpler to work with than the situation you wish to explore. We have to be careful that the simulation model matches the original situation as closely as possible. Otherwise the simulation results may not be a true reflection of the situation.
It will be possible to calculate the theoretical probability of the situations we will explore in this lesson. We then want to compare this theoretical probability with the results of the simulation which will give us the experimental probability. An example is done here to help you with the Investigation in your book.
Example
Run a simulation to determine the experimental probability of the following situation. You are a bomb disposal expert trying to diffuse a bomb. When the cover is removed there are six wires attached to the detonator. Cutting one of the wires will diffuse the bomb, cutting any of the other five will detonate it. If you have no idea which wire to cut, what is the probability you will successfully diffuse the bomb by randomly selecting a wire to cut?
Solution
The theoretical probability is straight forward. There are six possible outcomes only one of which favors success. Thus the theoretical probability is:
![]()
Determining the experimental probability by doing trials with the actual situation is really not a desirable option, we will set up a simulation. Any model that will give us six events, all of which are equally likely to occur, will serve our purposes. Some examples might be: rolling a six sided die; putting six colored marbles or six numbered pieces of paper in a bag and drawing one; spinning a spinner made from a circle with six equal sectors marked on it; using technology such as a calculator to pick one of six random numbers.
For this simulation let's use the TI83 to randomly select an integer from 1 to 6. We can pick any one of the integers from 1 to 6 to represent "success" and the other five integers will represent failure. Let's use 2 to represent success. If we run the simulation 5 times on our calculator we get:
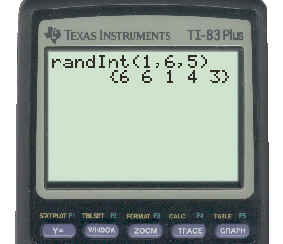
This is equivalent to a simulation of putting 6 pieces of paper with the integers 1 to 6 on them in a hat and drawing out one at a time, recording it, replacing it in the hat, and drawing again. The first time you drew a 6, the second time another 6, the third time a 1, the fourth time a 4, and the fifth time a 3. To see the TI83 keystrokes necessary to get this result click here.
In our five trials the integer 2, which represented success, did not appear. The number of "successful" trials was 0 and the probability of success is:
![]()
This is clearly not the same as what was expected since the theoretical probability was ![]() .
.
We can repeat the simulation using as many trials as we like. For example if we do the simulation with 25 trials we get:
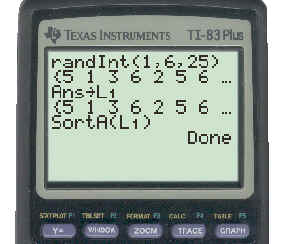
The results of the 25 trials have been stored in list L1 and sorted for easy counting. A display of results in list form is shown below:

To see the TI83 keystrokes necessary to get this result click here.
In our twenty five trials the integer 2, which represented success, appeared 5 times. The number of "successful" trials was 5 and the probability of success is:
![]()
Again this is not the same as the theoretical probability.
We could complete the simulation with more trials and compare that to the theoretical probability. However, that is what you are asked to do in a very similar problem in Investigation 1 in you text.
You don't have to use the calculator to do the simulation in Investigation 1. You can use any of the other methods suggested above. However, the calculator gives the trial results much quicker.
Activity
- Complete Investigation 1 on pages 303 & 304 in your text.
- Complete the Investigation Questions 12 & 13 on page 304.
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
Is it possible that the experimental probability found by doing a simulation will be exactly equal to the theoretical probability? Explain with an example.