Learning Resources

Lesson

Before you begin you might like to review the solution to Question 23 on page 239 in your text. It is very similar to this case study.

The first step in the solution of the case study is to draw a diagram containing circles and triangles. The work in this unit can then be applied to the problem. Consider a side view of the cone with the ball inside. It would look something like the diagram below:
                          

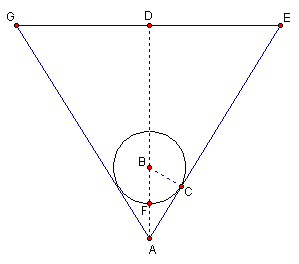
We need the dimensions of the cone, viz. its height (AD), slant height (AE) and the circumference of its base (GE is the diameter of the circular base).

1. From the given information, how long is AF? AB? BC?
2. BC  ^  AE because the ball touches (is tangent to) the cone. Use DABC, trigonometry, and the lengths from step 1 to find mÐ BAC.
3. From the given information, how long is AD (the altitude)?
4. Use the DADE  (note: AD  ^  GE),  trigonometry, and the information in steps 2 and 3 to find the length of AE, which is the slant height, and length of DE, which is the radius of the base of the cone.
5. Calculate the circumference of the base of the cone using the radius found in step 4.

The second part of the problem deals with cutting a sector from a circle and using what is left to make the cone. Again a diagram should be drawn similar to the one below:
                        

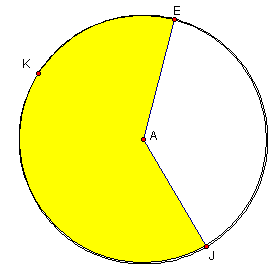
Think about cutting out the white sector and folding the yellow sector into a cone. It should be fairly obvious that the length of AE is both the radius of the circle and the slant height of the cone. It should also be obvious that is the circumference of the base of the cone. To see this more clearly, cut out a paper circle, remove a sector from it, and then fold what remains into a cone. Note the relation between the radius of the circle from which you cut the sector to form the cone and the slant height of the cone. Also note the relation between the length of the arc of the sector and the radius of the base of the cone.

6. Using the value of the slant height found in step 4 above, calculate the circumference of the circle from which the sector is cut .
7. Find the ratio of the circumference of the base of the cone (step 4) to the circumference of the circle (step 6).
8. Use this ratio to calculate the size of the angle of the sector to be used to make the cone.

If you have the time and interest, use the above as a  model to solve the Extension 1 problem.

Activity

Complete Case Study 1 and, depending on the time you have, complete the Extension 1 on page 278 in your text.

Test Yourself

There are no test items for the Case Studies.