Learning Resources

Lesson

If you have classmates at your site, it would be better to work together in groups of 2 or 3 to complete this investigation, as it will save you time and you can discuss and help each other. Also, be sure to record the answers to all the investigation steps in your own notebook.

There are two ways of completing this investigation. One is to use the method of paper-folding described in your text, the other is to use Geometer's Sketch Pad in the interactive window.

Text Book Method

To complete this investigation as described on pages 210 - 211 in your text you will need the following materials:

• a ruler
• a set of compasses to draw a circle
• a pair of scissors
• a protractor

Now get into groups, open your text to page 210 and try to complete as much of Investigation 2 as you can.  Some help and clues to doing the Investigation are provided, but use them only if you are having difficulty. If you do have difficulty, you might go here before contacting your teacher for help. Be sure to take turns making the folds in the paper and making the measurements. 

Alternate Method

For Part 1 of the Investigation, an alternate to paper folding for discovering the relation could be to use Geometer's Sketch Pad. To use this alternate method  simply click here.

For Part 2 of the Investigation, a similar alternate to the paper folding using Geometer's Sketch Pad is provided. To use this alternate method simply click here.

Do not proceed past this point unless you have done Investigation 2, either by the method presented in your text or by using the interactive windows with Geometer's Sketch Pad.

The key ideas of Investigation 2 are contained in Steps H, M, and N of the investigation. They are summarized below for your convenience. If you have completed the investigations as directed you should have discovered these important properties of chords in a circle.

There are several ways of stating this very important property. For example, you could use or state it in any of the following forms:

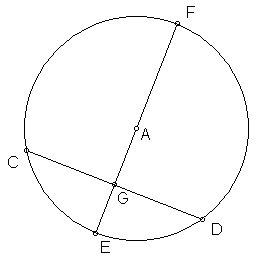
1. The perpendicular bisector of a chord of a circle always passes through the centre of the circle.

The above statement applied to figure on the right means:

If FE is the perpendicular bisector of CD (that is GC = GD and Ð FGC and ÐFGD are right angles)

Then, FE must pass through A the centre of the circle.

2. If a line passes through the centre of a circle and is perpendicular to a chord, then it will bisect the chord.

The above statement applied to figure on the right means

If FE passes through centre A and FE is perpendicular to CD

Then, GC = GD

3. If a line passes through the centre of a circle and bisects a chord, then it is perpendicular to the chord.

The above statement applied to figure on the right means

If FE passes through centre A and GC = GD

Then, FE is perpendicular to CD.

Activity

1. Complete the Investigation Questions 12 - 15 on page 211 in your text.
2. Do the CYU Questions 16 - 21 on page 212.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

1. You are given three non-collinear (not in a straight line) points, A, B, and C. Construct a circle that passes through all three.

The solution is presented as a Viewlet that will run automatically unless you pause it by clicking on the pause button which is the one marked II. After you pause, you can step through the frames by clicking on the advance button marked >>. To see the solution [click here].