Learning Resources

Lesson

A quadratic equation is an equation of the form ax² + bx + c = 0, where a, b, and c are real numbers and a ¹ 0. For example, 2x² + 7x - 15 = 0 is a quadratic equation.

This lesson will introduce you to finding the roots of these quadratic equations. A root is a value of x that makes the equation true. In the example above, -5 is a root because 2(-5)² + 7(-5) - 15 = 50 - 35 - 15 = 0. Thus -5 makes the equation true.

There are several methods of finding the roots of a quadratic equation. Three are described in this lesson (your text book refers to four but in fact two of them are just different methods of doing the same thing, viz. factoring). We will now look at each of these methods in turn.

Method 1: Graphing

First consider the relationship of the quadratic equation ax² + bx + c = 0 to the quadratic function y = ax² + bx + c. In fact, the equation is only the function with the y-value equal to zero. We refer to the values of x that make the y-value of any function equal to zero as the zeros of the function.

Thus the zeros of a quadratic function are the roots of the corresponding quadratic equation. But the zeros of a function can be found from its graph because all points on the x-axis have the y-coordinate equal to zero. Thus the x-intercepts are the zeros of the function and the roots of the corresponding equation.

This is shown below for the equation x² - x - 6 = 0. The graph of y = x² - x - 6 is drawn with its x-intercepts marked.

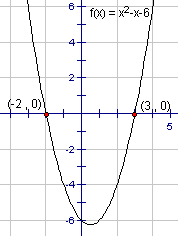
The zeros of the function are -2 and 3. These are also the roots of the equation (substitute them in to the equation to check).

We will use the TI83 to graph the function corresponding to a given equation. We can then use either the [TRACE] feature and scroll until we come to the x-intercept or we can use the [CALC] and 2:Zero feature to have the calculator locate the intercept for us.

If we use the TI83 to find the roots of 4x² + x - 3 = 0 we get the result below:

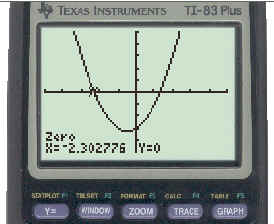
To see the keystrokes necessary to get this result click here.

One of the roots of the equation 4x² + x - 3 = 0 is -2.302776. Try substituting this into the equation to check that it works. Then use your calculator to find the other root of this same equation.

Method 2: Factoring

Using factoring to find the roots of a quadratic equation relies on the Principle of Zero Products. This principle states that if the product of two numbers is zero, then one or both of the numbers must be zero. For example, this means:

If , then a = 0 or b = 0

OR

If (x - 4)(2x + 5) = 0, then x - 4 = 0 or 2x + 5 = 0

Note that (x - 4)(2x + 5) = 0 is the same as writing 2x² - 3x - 20 = 0. But this is a quadratic equation. We can thus solve any quadratic equation if we can rewrite it as a product of two factors. Consequently, it is to factoring quadratics that the rest of this part of the lesson is devoted.

Factoring Using Algebra Tiles

Note that the use of algebra tiles is efficient only when they are used to form a square or rectangle with numbers that are not very large. When the values are decimals or fractions the tiles are not very useful at all.

Recall your experiences with these tiles from earlier mathematics courses. In Mathematics 1204 you learned to factor expressions using algebra tiles (see Pages 134 to 140 of Mathematical Modeling: Book 1), so this should really be only a review of the concepts for you. At this level you should be beyond having to use algebra tiles to help you factor. However, if you need the practice, read through this section in Focus F of your text.

Factoring by Decomposition

You only need to use the method of decomposition when you don't see the pattern of the factors directly. If you can factor by inspection, guessing, trial and error, or whatever method, and it is efficient, use it. For example, you may need no "special tricks" to factor trinomials when the coefficient of the squared term is one. You simply look for two numbers whose product is the constant term and whose sum is the coefficient of the x-term. Some examples are shown below - look for the pattern.

x² + 5x + 6 = (x + 3)(x + 2) {3 x 2 = 6 and 3 + 2 = 5}

x² +6x + 5 = (x + 1)(x + 5) {5 x 1 = 5 and 5 + 1 = 6}

x² - x - 6 = (x - 3)(x + 2) {-3 x 2 = -6 and -3 + 2 = -1}

x² - 5x - 6 = (x + 1)(x - 6) {-6 x 1 = -6 and -6 + 1 = -5}

When the coefficient of the squared term is not one, it may not be so easy to "see" the factors directly. It is then that we use the method of decomposition.

This method is shown in your text book on page 43 and another example is given in the interactive below.

It is not always possible to factor a trinomial, even with decomposition. In those cases we need another method.

Method 3: Completing the Square

Before we look at an example of using this method, it is important to review some notation. The symbol means to take the principal or positive square root of a number, thus for example . But we know that 4 has two square roots, 2 and -2.

Applying this to a simple equation we have:

Note the necessity of using the sign in front of the sign. This is to show both square roots of the number, not just the principal square root.

Consider the following equation:

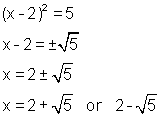
Again note the necessity of using the sign.

There is an example in your text showing this method. That example can be solved by factoring, but the method of completing the square is used to show the procedure. The example in the interactive below cannot be solved by factoring using decomposition. The procedure for solving by completing the square is nonetheless the same.

When the coefficient of the squared term is not equal to one, we first make it equal to one by dividing through by it (or multiplying by its reciprocal). This is shown in the example in the interactive below.

There are some problems in the assigned work that require knowledge and skills about rational expressions before you can use the concepts of quadratics presented in this lesson.

Question 17 on page 47 of your text assumes you have skills with rational expressions that you may not have. The example in the interactive below shows one approach you can take to solving these type of equations.

Activity

1. Read through the examples in Focus F on pages 41 - 43 in your text.
2. Complete Focus Questions 1 - 5 on pages 43 & 44.
3. Do the CYU Questions 8 - 12; 15 -19; 21; 22 on pages 44 - 47

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

After you do the assigned activities, click on the Test Yourself button at the top of the page for a quick quiz on this lesson.

Test Yourself

1. Solve the equation 6x² + 13x - 5 = 0 by each of the three methods: graphing, factoring, completing the square.
2. The Port aux Basques Recreation Commission plans to add a swimming pool onto its sports complex and at the same time widen the existing arena. If the present arena is 30 meters by 20 meters and its area is doubled by adding a strip at one end and a strip with the same width along one side, find the width of the strip required.