Learning Resources

Outcomes

In this lesson you will learn

• Solve quadratic equations using a variety of methods including finding the x-intercept of the graph of the corresponding function, analyzing tables of values, guessing and checking, factoring (using algebra tiles if necessary), and completing the square.
• Explore the connection between the x-intercepts of the graph of a quadratic function, the zeros of the function, and the roots of the quadratic equation formed by setting the function equal to zero.
• Solve maximum and minimum problems as well as find the roots of quadratic equations.

By the end of this section you should be able to:

• Derive and apply the quadratic formula.
• Solve quadratic equations.
• Relate the nature of the roots of quadratic equations and the x-intercepts of the graphs of the corresponding functions.
• Represent non-real roots of quadratic equations as complex numbers.
• Demonstrate an understanding of the role of irrational numbers in applications.
• Demonstrate an understanding of the nature of the roots of quadratic equations.

Introduction

In this section you will examine several methods of finding the roots of quadratic equations. These include graphing, factoring, and completing the square. By locating the roots, you will solve problems involving quadratic functions. This work will provide a background for the derivation and application of the quadratic formula which is used to find the roots of any quadratic equation that can be written in the form .

You will use the quadratic formula 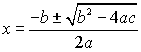   to determine whether the roots of a given quadratic equation are two different real roots, two equal real roots, or two imaginary roots.

This section should take you about 6 hours to complete.

Prerequisites

To be successful in this lesson, it would be helpful to know the following:

• How to factor and expand quadratic expressions.
• How to use completing the square to create quadratic expressions.
• How to solve linear equations.