Learning Resources

Lesson

We will begin this lesson by looking at some of the terminology used to describe parabolas. You may have already learned that the graph of any quadratic function is a curve called a parabola. A parabola has a maximum or minimum value and the point where the maximum or minimum occurs is called the vertex. Every parabola has an axis of symmetry that passes through the vertex and is perpendicular to the x-axis. This is all shown on the diagram below:

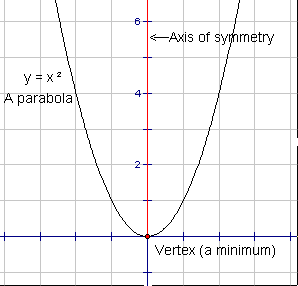
Previously you studied all parabolas as transformations of the basic quadratic function y = x² . You learned that the transformational form of a quadratic function could be written as:

First recall that replacing x by h - h translated the function horizontally by h units and replacing y by y - k translated the function vertically by k units. This is shown in the interactive below.

You should also recall that multiplying y by the factor "stretched" the parabola vertically by a factor of a. This is shown in the interactive below.

One of the chief advantage of the transformational form is that it can be used to sketch the graph fairly quickly.

We can use the transformational form of the equation to sketch a graph by deriving a table of values for a given function based on the translation and stretching of the graph of y = x². This is shown in the example below.

Example:

Use your knowledge of transformations to sketch the graph of
2(y + 1) = (x - 2)²

Solution:

The graph of y = x² is translated 2 units to the right and 1 unit down. There is a vertical stretch of ½ . Using mapping notation to describe this transformation we get:

We can now use this to make a table of values for the new function and plot its graph. That is shown in the interactive below.

Now that we have reviewed the transformational form, we will study two other forms for the equation of a quadratic function.

We now want to consider two other forms of the quadratic function. The first one we shall consider is called the standard form. It is written as:

Note that the standard form is very similar to the transformational form. It is important that you be able to convert from one form to the other. An example of how to do this is shown below:

We want to examine the graphs of several quadratic functions written in standard form to determine what information about the graph is conveyed by the values of a, h, and k. More specifically, we are interested in the coordinates of the vertex, the equation of the axis of symmetry and the direction of opening of the parabola. Several problems in your text lead you to discover this relation. The interactive below should also help you to discover the same relation. Remember to compare the graphs to the graph of the basic function
y = x²

Study the examples above very closely. Do you see a relation between a, h, and k in the equation and the vertex, axis of symmetry and direction of opening of the parabola? You will learn more about this as you do the exercises in your text book.

We now want to look at the general form of the equation.

The general form for the equation of a quadratic function is:

y = ax² + bx + c

As with the standard and transformational forms of the equation, this form provides some information about the graph of the corresponding parabola. There are several problems in your text that lead you to discover this information. Also you should see the relation by studying the graphs in the interactive below. Remember to compare all graphs to the graph of the basic function y = x².

The next page contains a summary of the information and use of each of the forms of the quadratic function.

You should have reached the following conclusions about the different forms of the quadratic function:

• The transformational form allows you to read the vertex and the vertical stretch factor easily. It also allows you to sketch the graph quickly by generating a table using the mapping rule.
• The standard form allows you to read the vertical stretch, locate the vertex, and enter the function into the graphing calculator easily so that its graph can be drawn electronically.
• The general form is the one with the least amount of information about the properties of the parabola. It gives the vertical stretch and y-intercept. It is the form given by the graphing calculator when regression is done, so you should be familiar with it.
• Direction of opening can be determined from all three forms by looking at the sign of a.

Activity

1. Complete Focus C on pages 24 - 29 in your text.
2. Complete Focus Questions 1 - 5 on pages 29 & 30.
3. Do CYU Questions 6 - 11 on pages 30 & 31.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

After you do the assigned activities, click on the Test Yourself button at the top of the page for a quick quiz on this lesson.

Test Yourself

The function is in transformational form.

1. Describe the transformations of the graph of y = x² that are necessary to get its graph.
2. Sketch the graph using these transformations.
3. Write the function in standard form and use it to verify the coordinates of its vertex.
4. Write the function in general form and state the y-intercept.
5. Write the function using the mapping rule.

Solution