Focus C: Forms of Quadratic Functions
Test yourself (Answers)
- To get the graph of
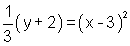we can first apply a vertical stretch factor of 3. This makes the
parabola narrower, e.g. it moves the point (1 , 1) up to (1 , 3),
it moves the point (2 , 4) up to (2 , 12), etc. The vertex of (0 , 0) is
not affected by a stretch.
We can then translate the stretched graph of y = x2
horizontally 3 units to the right and vertically 2 units downward.
Applying this translation to the vertex of (0 , 0), we get the new vertex at (3 , -2).
-
-
To write the equation in standard form, we multiply through by 3 to
eliminate the fraction and then subtract the 2 from both sides as shown
below.
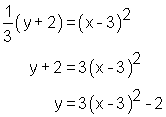
This form also shows the vertex to be at (3 , -2) and the vertical
stretch factor to be 3. The equation of the axis of symmetry is x = 3.
-
Start from the standard form, expand the binomial, and rearrange to
write the equation in general form. This is shown below.
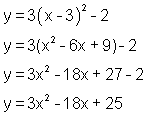
This form shows that the y-intercept is 25, and again the
vertical stretch factor is shown to be 3.
- In mapping notation the function becomes:
|
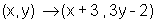
