Learning Resources
Activity
1. For each of the following, find (
)(x) and (
)(x). Give the domain
of each.
(a) f(x) = 3x ; g(x) = -2x + 1
(b) f(x) = 2x2 - x + 1 ; g(x) = x + 3
(c) 
; g(x) = 20x - 16
(d) f(x) = - 2x3 ; g(x) = 2x + 1
(e) 
; g(x) = -x + 1
(f) 
; 
(g) 
; 
2. Use the graph of f(x) and g(x) shown below to find each of the following if possible. If not possible, explain why.
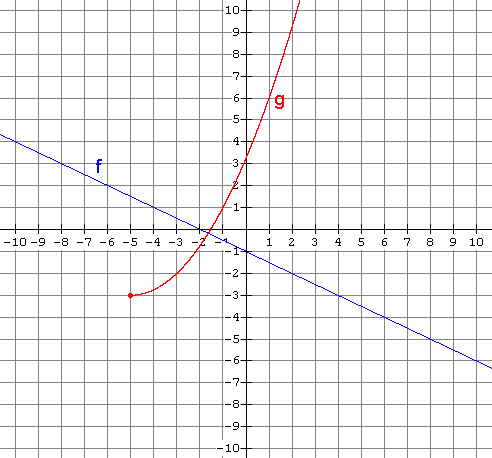
(a) ()(-3) (d) ()(-4)
(b) ()(1) (e) ()(8)
(c) ()(-5) (f) ()(10)
3. Show algebraically which, if any, of the following pairs of functions are inverses
of each other.
(a) f(x) = 3x - 6 ; g(x) = 
(b) 
; 
(c) 
; g(x) = 
(d) f(x) = x2 + 2x + 3 ; 
(e) f(x) = (x + 1)3 ; 
4. Sketch a graph of the inverse of each of the functions graphed below and tell whether the inverse is also a function.
(a)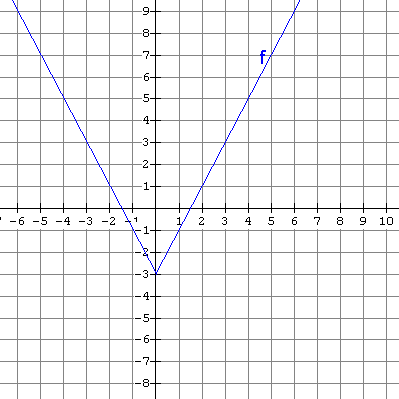 
(b) 
5. For each of the following functions,
(i) find its inverse and when the inverse is a function, write it using the inverse
function notation; if the inverse is not a function, give a restriction of the
domain of the original function that would make the inverse a function, and
then write the inverse for this restricted function using inverse function
notation;
(ii) sketch the graph of the function (or the function with the restricted domain)
and the inverse function on the same set of axes.
(a) f(x) = -3x +2
(b) 
(c) 
(d) f(x) = 2x2
(e) 
(f) h(x) = 5x2 - 10x + 5
(g) p(x) = x2 - 2x - 4
Test Yourself
1. For each of the following, find ()(x) and ()(x). Give the domain
of each.
(a) 
; g(x) = 3x + 2
(b) 
; g(x)=3x-1
(c) 
; 
2. Use the graph of f(x) and g(x) shown below to find each of the following if possible. If not possible, explain why.
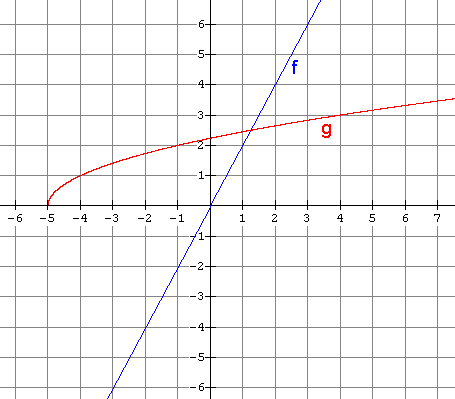
(a) ()(-5) (d) ()(-3)
(b) ()(-1) (e) ()(-2)
(c) ()(4) (f) ()(2)
3. Show algebraically which, if any, of the following pairs of functions are inverses of each other.
(a) f(x) = 2x - 6 ; 
(b) 
; g(x) = (x + 2)3
(c) f(x) = x2 ; 
4. Sketch a graph of the inverse of the function graphed below and tell whether the inverse is also a function.
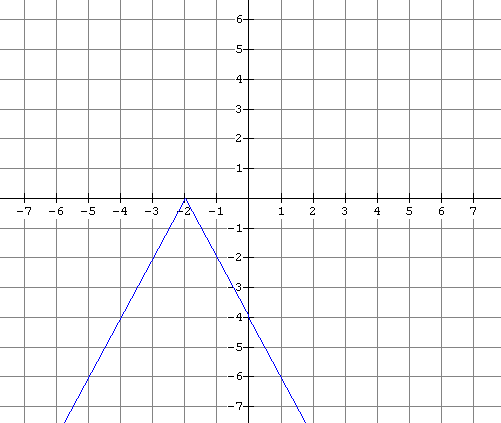
5. For each of the following functions,
(i) find its inverse and when the inverse is a function, write it using the inverse
function notation; if the inverse is not a function, give a restriction of the
domain of the original function that would make the inverse a function, and
then write the inverse for this restricted function using inverse function
notation;
(ii) sketch the graph of the function (or the function with the restricted domain)
and the inverse function on the same set of axes.
(a) 
(b) f(x) = 2(x + 2)2 - 3
(c) f(x) = x2 - 6x + 7