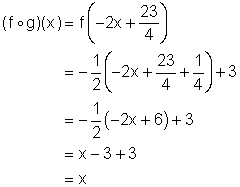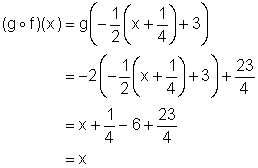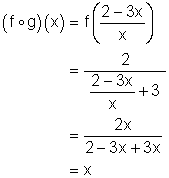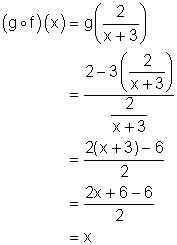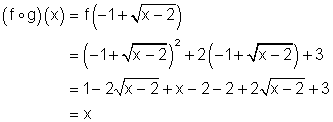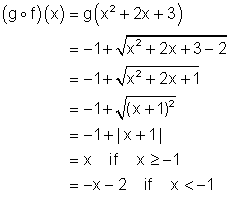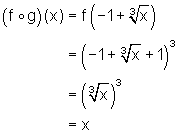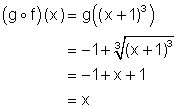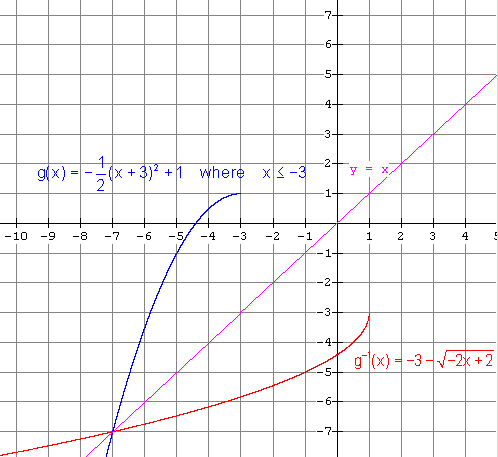Learning Resources

Review (Answers)

1. (a) ()(x) = -6x + 3 ; Domain = {x | x is a real number}
()(x) = -6x + 1 ; Domain = {x | x is a real number}

(b) ()(x) = 2x² + 11x + 16 ; Domain = {x | x is a real number}
()(x) = 2x² - x + 4 ; Domain = {x | x is a real number}

(c) ()(x) = -5x + 4 ; Domain = {x | x is a real number}
()(x) = -5x - 16 ; Domain = {x | x is a real number}

(d) ()(x) = -2(2x + 1)³ = -16x³ - 24x² - 12x - 2 ;
Domain = {x | x is a real number}
()(x) = -4x³ + 1 ; Domain = {x | x is a real number}

(e) ()(x) = ; Domain =
()(x) = ; Domain =

(f) ()(x) = ; Domain =
Note: If you rationalize the denominator of this expression you get: ()(x) = . However, recall that these expressions are only equivalent when x ¹ 4. Thus these functions have a slightly different domain, viz. Domain = . Thus this is a case where it is not appropriate to rationalize the denominator.

()(x) = ; Domain = {x | x > - 2}

(g) ()(x) = ; Domain =

()(x) = ;Domain =

2. (a) ()(-3) = 0

(b) ()(1) = -4

(c) ()(-5) =

(d) ()(-4) = 6

(e) ()(8) = -3

(f) ()(10) = Not possible because f(10) = -6 and g(-6) is undefined

3. (a) ()(x) = f(g(x)) =
()(x) = g(f(x)) =
Since the composition of the functions gives x, the functions are inverses of each other.

(b)

Since the composition of the functions gives x, the functions are inverses of each other.

(c)

Since the composition of the functions gives x, the functions are inverses of each other.

(d)

Since the composition of the functions gives x only when x ³ -1, the functions are NOT inverses of each other.

(e)
Since the composition of the functions gives x, the functions are inverses of each other.

4. (a)

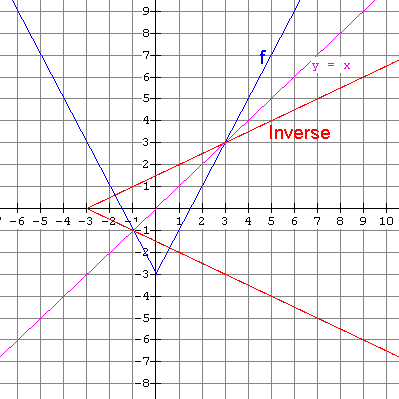
Inverse is NOT a function.

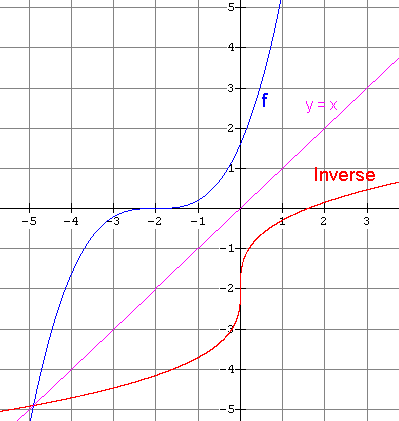
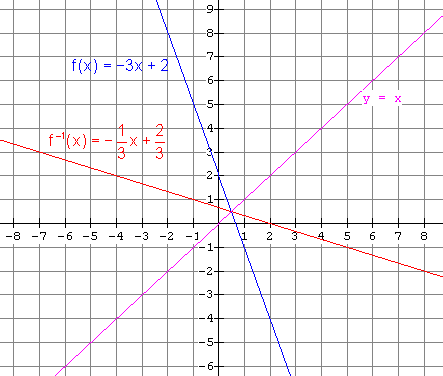
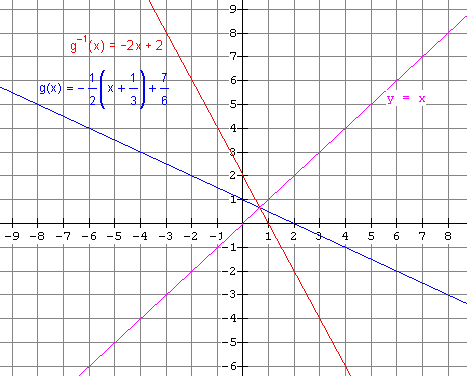
(b)

Inverse is a function.

5.(a) (i) The inverse is a function. It is:

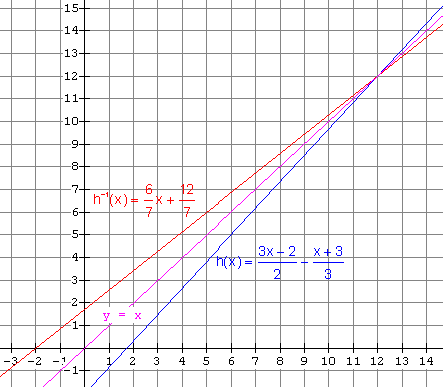
(ii)

(b) (i) The inverse is a function. It is

(ii)

(c) (i) The inverse is a function. It is

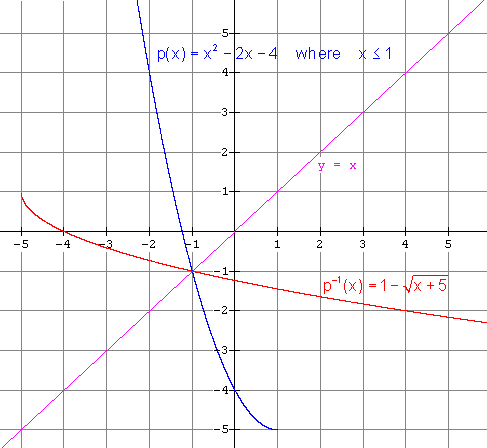
(ii)

(d) (i) The inverse is NOT a function. It is

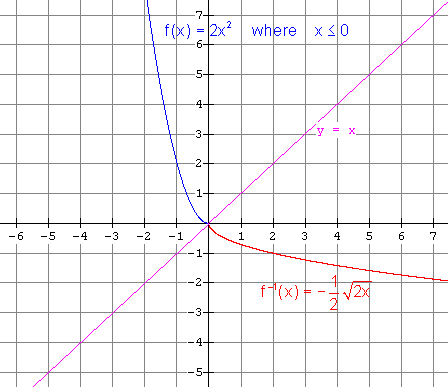
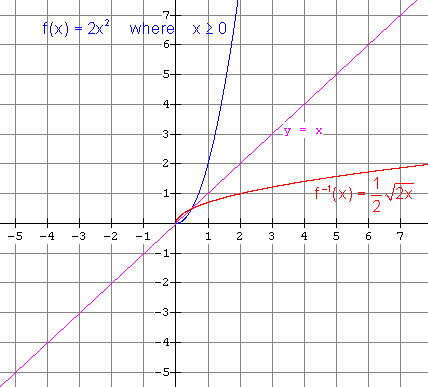
(ii) Restricted function: x £ 0 gives

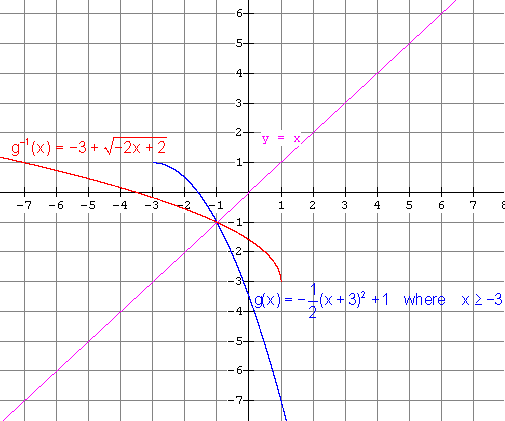
Restricted function: x ³ 0 gives

(e) (i) The inverse is NOT a function. It is:

(ii) Restricted function: x £ -3 gives

Restricted function: x ³ -3 gives

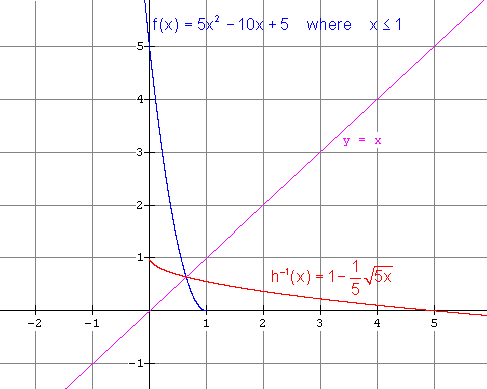
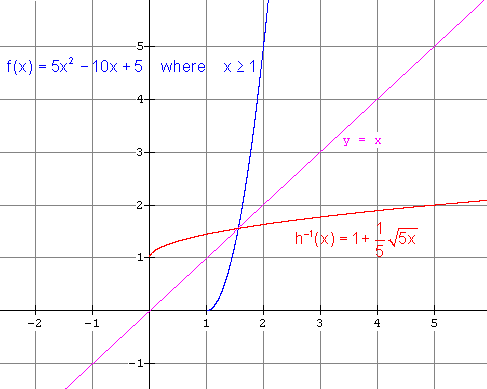
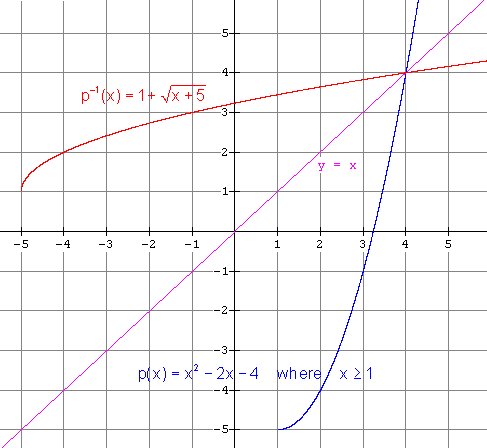
(f) (i) The inverse is NOT a function. It is

(ii) Restricted function: x £ 1 gives

Restricted function: x ³ 1 gives

(g) (i) Inverse is NOT a function. It is

(ii) Restricted function: x £ 1 gives

Restricted function: x ³ 1 gives