Learning Resources
Lesson
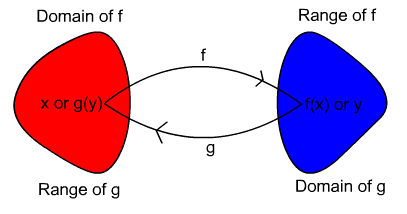
Definition: Two functions f(x) and g(x) are inverses of each other if and only if
(
)(x) = (
)(x) = x for all x in the domains of f and g.
This can be represented by a mapping diagram as follows:
You have dealt with the concept of inverses before in relation to arithmetic operations. For example, subtraction is the inverse of addition, thus if 7 is added to any number, x, and then 7 is subtracted from the result, you get back to the original number x.
Think of the inverse as an "undoing" of some previous operation. It may be related to mathematics or some real world situation. For example, taking off a jacket is the inverse of putting on a jacket; turning off a car is the inverse of starting a car; etc.
The example below shows this concept for a simple function.
Example
Show that f(x) = 2x - 3 is the inverse of g(x) = 
Solution
()(x) = f(g(x)) = 
()(x) = g(f(x)) = g(2x - 3) = 
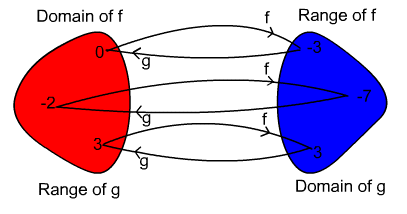
Now consider a particular case:
Start with 7 in the domain of f, then f(7) = 2(7) - 3 = 11
Now find g(11), g(11) = 
= 7
We started with 7, applied the two functions in composition and ended up with 7.
A mapping diagram of a few particular values gives:
Example 2
Are the functions h(x) = (x - 2)3 and p(x) = 2 + 
inverse functions? Explain.
Solution
h(p(x)) = h(2 + ) = ((2 + ) - 2)3 = ()3 = x
p(h(x)) = p((x - 2)3) =2 + 
= 2 + (x - 2) = x
Since h(p(x)) = p(h(x)) = x , the functions are inverses of each other. We started with x and applied the composition of the two functions and ended up with x. The second function "undoes" what the first function "does".
Example 3
Are the functions f(x) = (x - 1)2 + 2 and g(x) = 1 + 
inverse functions? Explain.
Solution
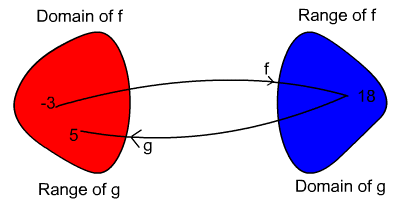
Consider the case when x = -3
f(-3) = (-3 - 1)2 + 2 = 16 + 2 = 18 and g(18) = 1 + 
= 1 + 4 = 5
Thus g(f(-3)) = 5 , but if they were inverse functions g(f(-3)) must equal -3, so they are not inverse functions. This is shown in the mapping diagram below.
If two functions are inverses of each other, the range values of one become the domain values of the other. If we think of a function, f , as a set of ordered pairs
(x , y), then its inverse function, g , is the set of ordered pairs (y , x). That is we simply interchange the x and y coordinates of both functions.
Example 1
(a) Graph the linear function f(x) = 4x + 1 by making a table of values of at least five points.
(b) Make a table of values for g, the inverse of f, by interchanging the coordinates in the table in (a) and plot them on the same axes. Sketch the graph through these points.
(c) What is the relation between the two graphs?
Solution
We will now use the relation between the graph of a function and the graph of its inverse, which was shown in Example 1 above, to sketch the graph of the inverse of any function whose graph is known.
Example 2
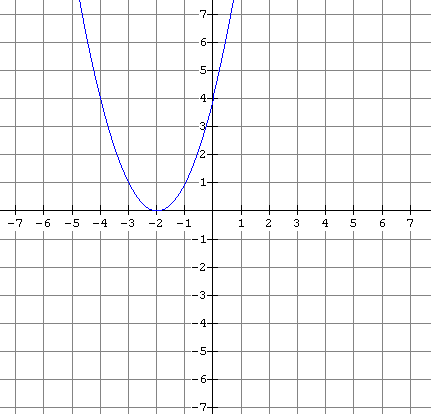
Sketch the graph of the inverse of the function whose graph is given below.
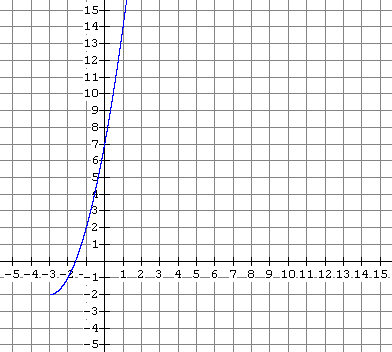
Solution
Note that in the above example we did not need the algebraic form of the original function in order to sketch its graph.
Activity
Show algebraically which, if any, of the following pairs of functions are inverses of each other.
1. f1(x) = 2x + 4 and f2(x) = 
2. f1(x) = 3(x - 1) + 2 and f2(x) = 
3. f1(x) = 3(x + 2) and f2(x) = 
4. f1(x) = (x - 1)3 and f2(x) = 
5. f1(x) = x3 + 2 and f2(x) = 
6. f1(x) = 2(x - 1)3 + 4 and 
7. f1(x) = (x - 3 )2 and f2(x) = 
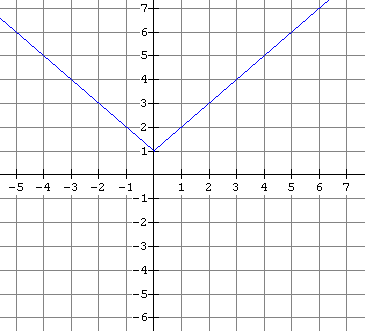
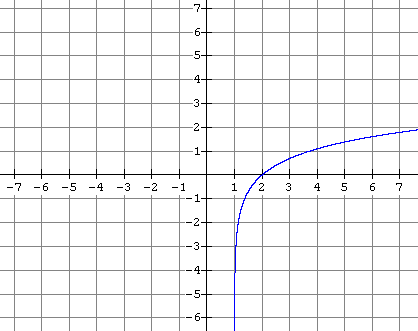
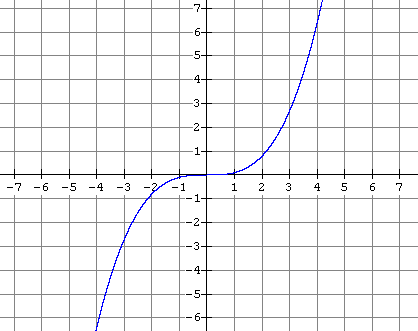
Sketch a graph of the inverse of each of the functions graphed below and tell whether the inverse is also a function.
8. 
9. 
10. 
Test Yourself
Show algebraically which, if any, of the following pairs of functions are inverses of each other.
1. f1(x) =2x - 3 and f2(x) = 
2. f1(x) = 3(x+2) - 5 and f2(x) = 
3. f1(x) = (x + 2)3 and f2(x) = 
Sketch a graph of the inverse of each of the functions graphed below and tell whether the inverse is also a function.
4. 
5. 