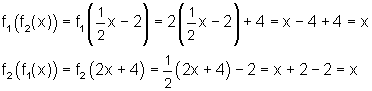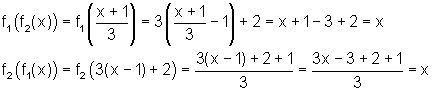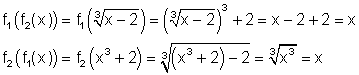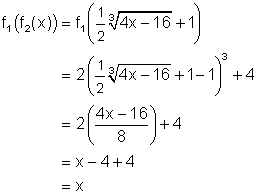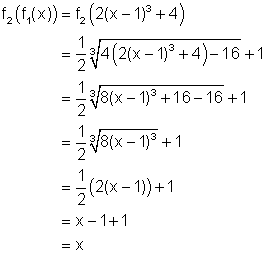Learning Resources

Inverse Functions Defined

Answers to Activities Questions

1.

Since the composition of the functions gives x, the functions are inverses of each other.

2.

Since the composition of the functions gives x, the functions are inverses of each other.

3.

Since the composition of the functions does not give x, the functions are not inverses of each other.

4.

Since the composition of the functions does not give x, the functions are not inverses of each other.

5.

Since the composition of the functions gives x, the functions are inverses of each other.

6.

Since the composition of the functions gives x, the functions are inverses of each other.

7.

When x ³ 0, which indicates inverses

However, when x < 0 , which means the functions are not inverses.

For example,

Thus we can say that these functions are NOT inverses of each other unless we restrict the domain of f₁ to x ³ 0.

8.

Applying the vertical line test we can see that the inverse is not a function. For example, points (3 , 2) and (3 , -2) are both on the graph and they have the same x-coordinate, hence not a function.

9.

Applying the vertical line test we can see that the inverse is a function.

10.

Applying the vertical line test we can see that the inverse is a function.